非專業立體機動裝飾研究報告
本篇是看過【閒聊】人體承受立體機動裝置的加速度之後,覺得此篇有趣,會略有不足,所以作出一次推論和估算
純為興趣之作,切勿當真
本人不負責任何因計算或推導錯誤所引起或產生之任何意外。
2013年7月18日
近來大熱之「進擊之巨人」,相信不少人有看過。對於其「蜘蛛俠」式的「立體機動裝置」來移動的設定,相信亦有不少人趨之若鶩,想來說一說,好,本文就用我現學現查現賣的物理和數學知識,去分析「立體機動裝置」的真相。
艾倫的行進方式
巨人們的可怕,相信經歷過多次入侵的艾倫就最清楚不過。「立體機動裝置」最大的用途,是用來對付身高比人類高很多,但弱點只有後頸一小部分的巨人們。為了補足人體的身高不足,迫不得以用繩(鋼纜?)盪來盪去繞到巨人後頸位置,作出致命一擊。
但巨人們極難對付,每次外查的調查兵團只有10%的人可以回來。所以實際操作上,「立體機動裝置」最大的用途,應當是繼馬匹之外,最有效的保命逃跑工具。
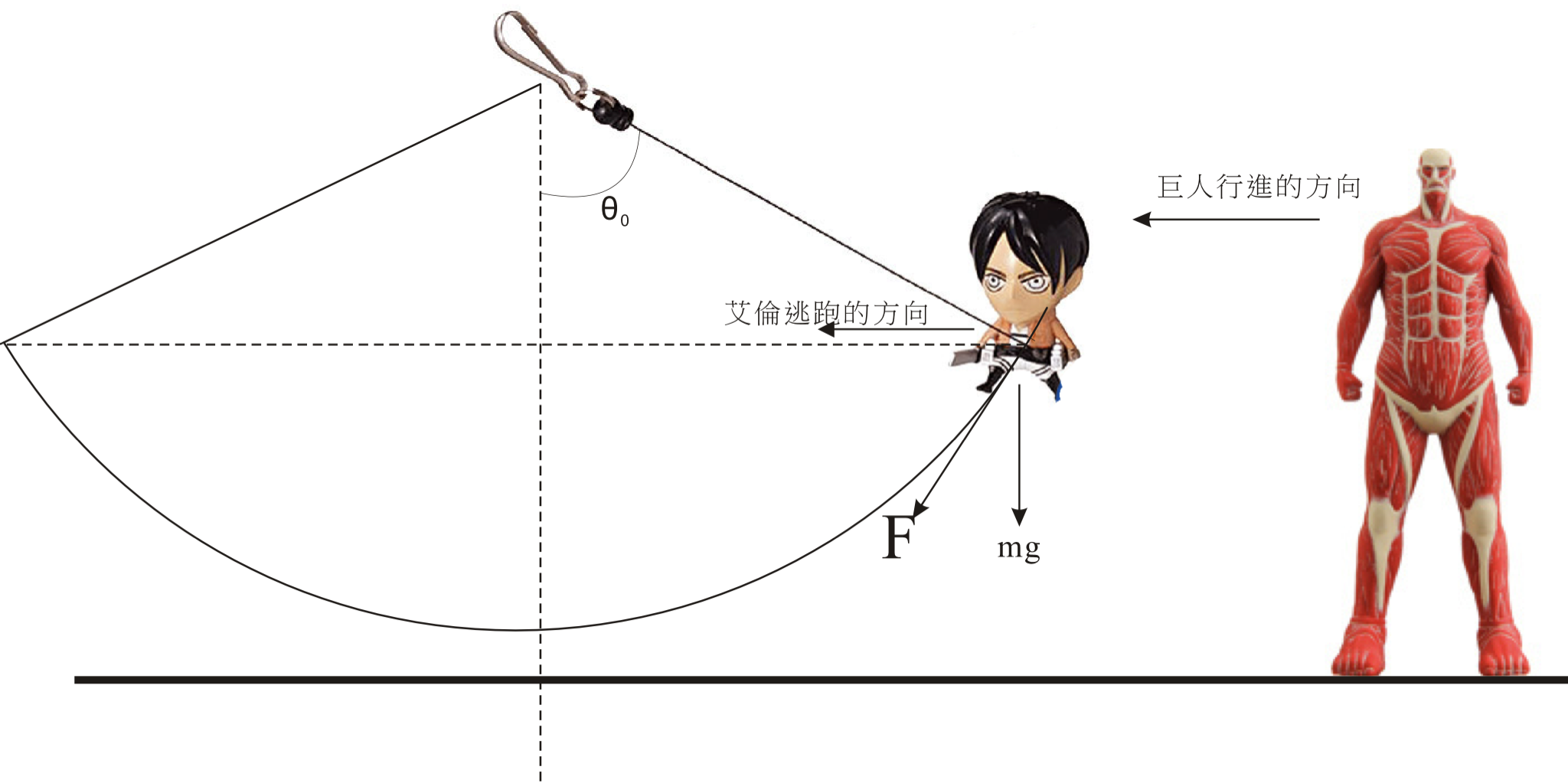
根據維基百科所示:
假設繩索是無重量,不拉長,一直綳緊;
Motion為2D,鐘擺行程為一弧而非橘圖形;
沒有能量流失,忽略空氣阻力和阻力。
則,可得出一條微分方程:
其中g為地球重力加速度:
已知鐘擺會由位能-->動能-->位能
位能轉變:
動能轉變:
因為假設沒有能量流失,所以,在每一個角位移(
轉成用角位移來表示則為:
(一般中學所學應為:
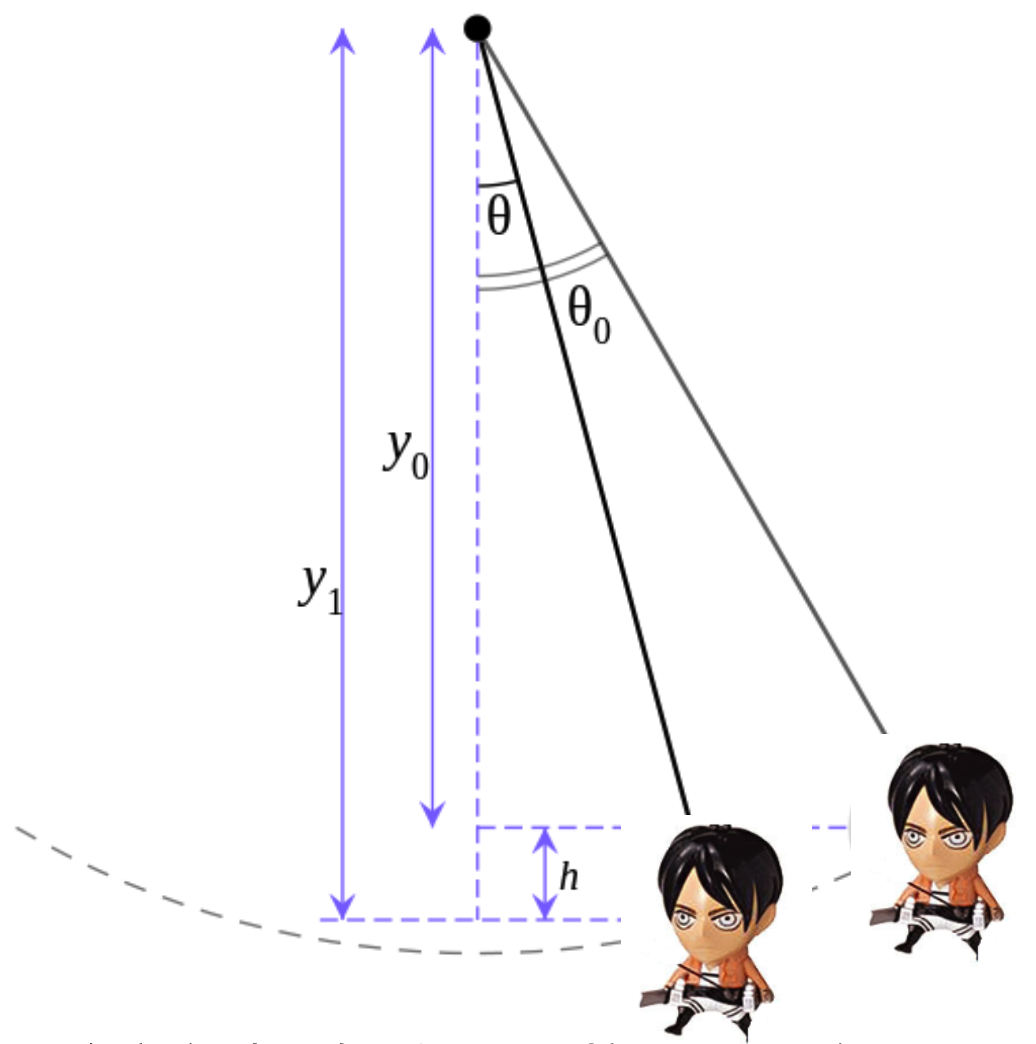
如圖所示,
又,
所以,
代入上式:
中學有學過鐘擺原理,而鐘擺週期為:
但上式是基於
將上式上下倒轉:
擺動一個周期,角度變化應為:
可以簡化為:
所以,角度由
好,這條不是人類能理解的積分式,所以我直接複製維基百科的答案:
其中,
所以,用人類的語言來說,
而艾倫逃走方向等於巨人前進方向(即水平方向),為簡單計算水平方向的前進速度,用每半個鞦韆水平方向的位移,除半個周期:
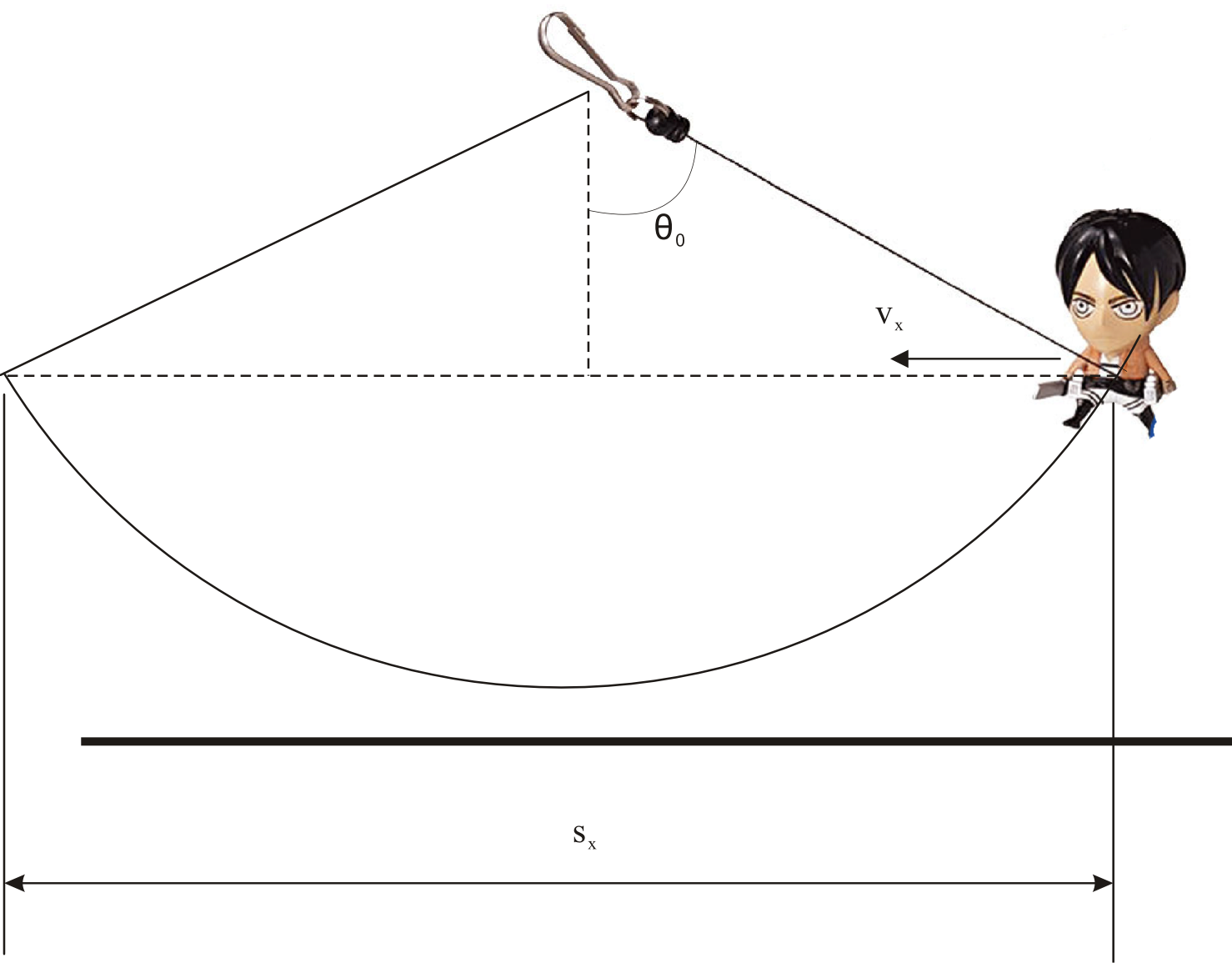
水平方向的位移總量有:
所以水平方向逃跑速度:
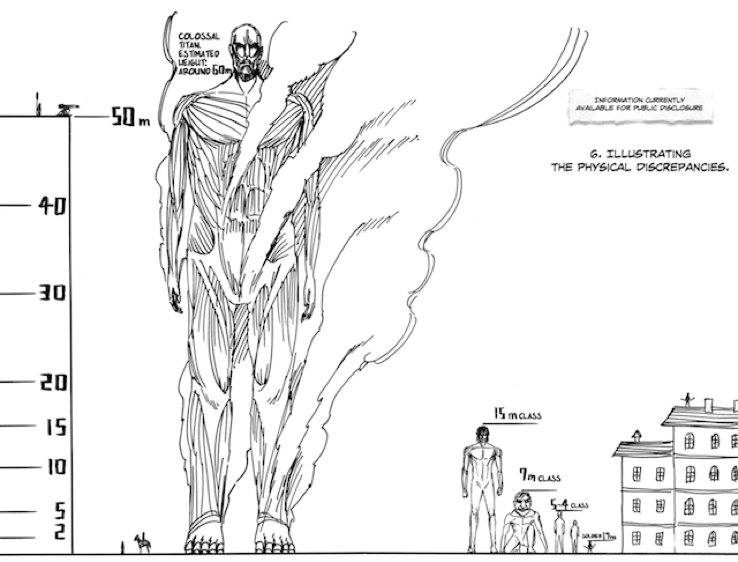
根據書中所載,60m級數的巨人只出現過兩次(註: 寫這篇研究時,漫畫內容才進入到艾倫奪還戰)。就假設一般都是和巨人化的艾倫一樣都是15m高的級數。那繩索長度按理就不會準備得太長,而且據書中和動畫所見,都是約4-5層樓高。
就假設繩索長
初始角度
將公式輸入wolframalpha.com (原來維基百科和wolfram對於K(k)的定義不一樣,差了一個二次方….各位如想代入請注意),得出
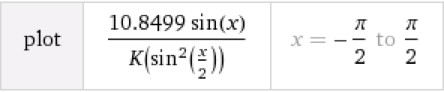
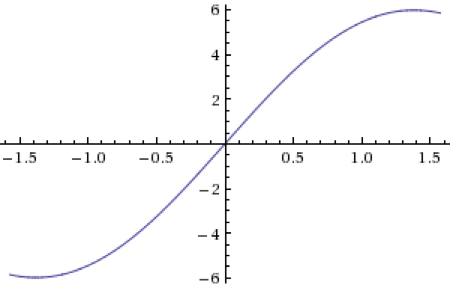
上圖橫軸為
由此得出,當
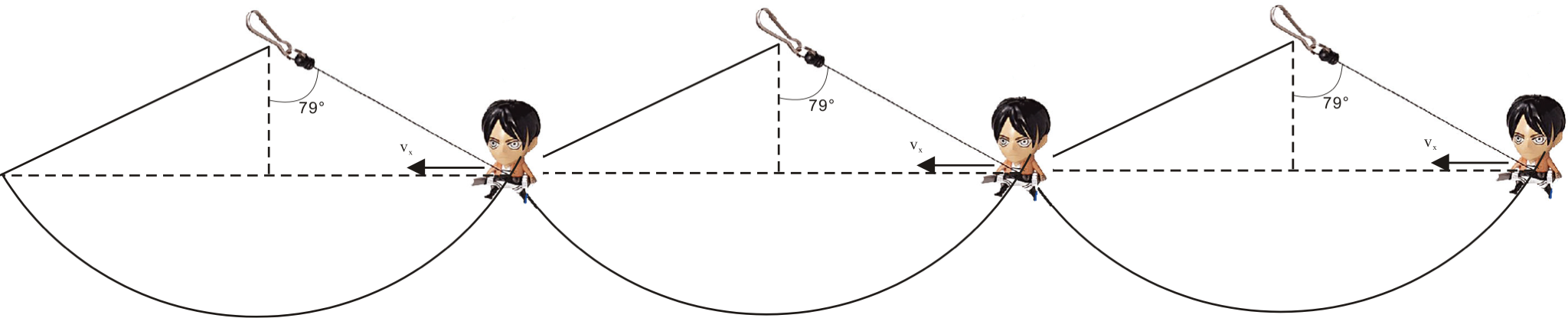
即,艾倫最佳的行進方法應為: 向前方傾角
但話說回來… 好慢呀…
水平前進的平均速度最大值只有

怎樣才能保命?
那到底要用怎樣的方法來前進才可以保命呢?在還沒研究氣動裝置之前,就讓我試用所有方法去幫助艾倫逃跑吧。
首先得推測逃跑的速度。在漫畫中所見,馬匹是繼「立體機動裝置」外唯一能逃跑的工具。那就是說,艾倫的逃跑速度至少要跟馬匹一樣。上wolframalpha.com一查,原來馬匹陸上行走最高速度是

那原來艾倫他們的行進方式應為這樣:

根據維基百科對拋體運動(Projectile motion)所示:
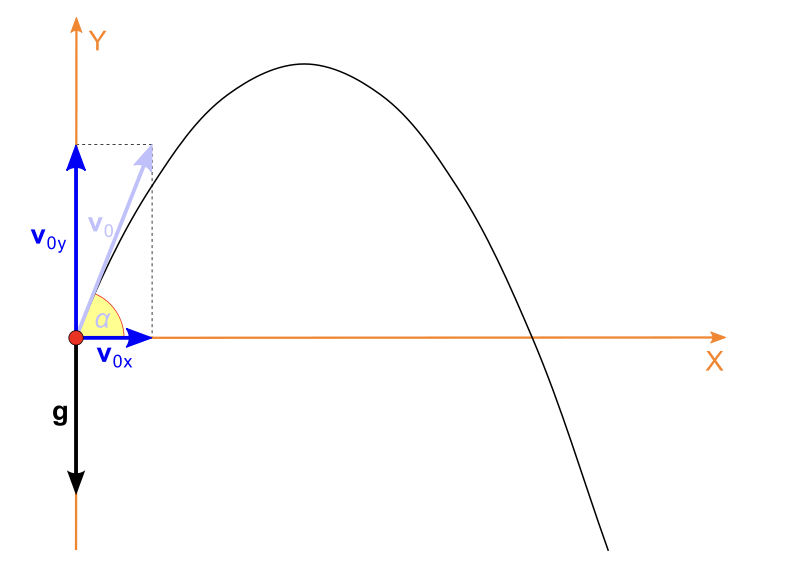
假設以
其中
那麼,水平和垂直的加速度則是:
而水平和垂直的位移則是:
假設最遠的水平距離為
這時候,最遠水平距離
當
所以投射角應為
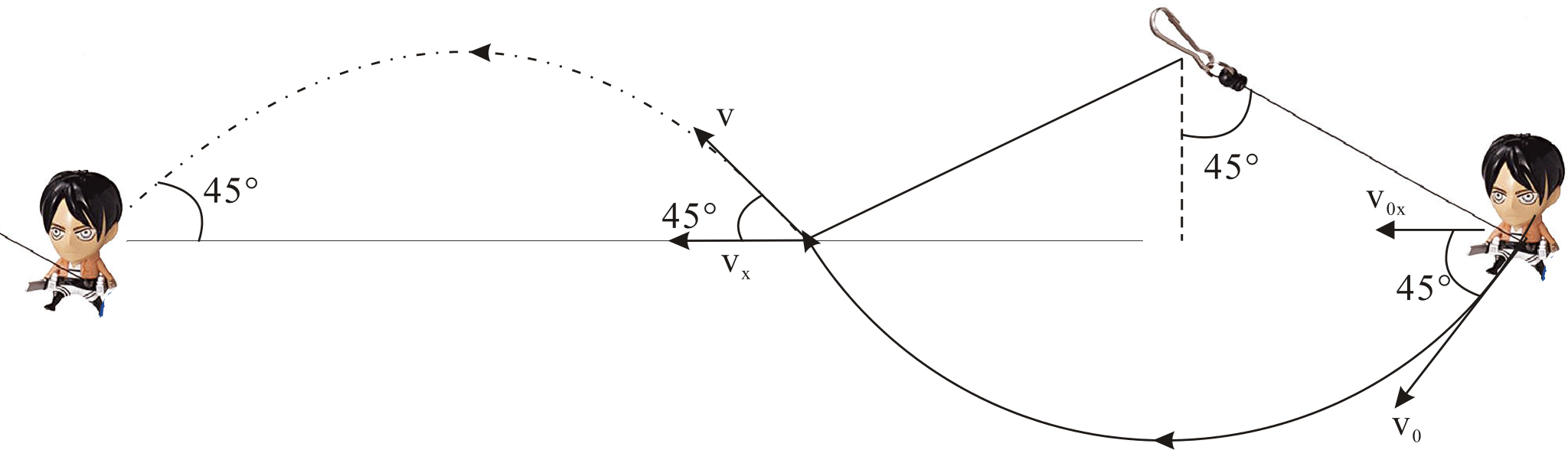
如上圖,拋體的拋出角度為
如果動能和勢能的轉換中能量沒有流失,那麼
如果沒有了氣動裝置,則艾倫就需要以
先不論氣動裝置如何幫忙艾倫達到這速度,現在先來研究一下在這情況下人體所受的繩索拉力。
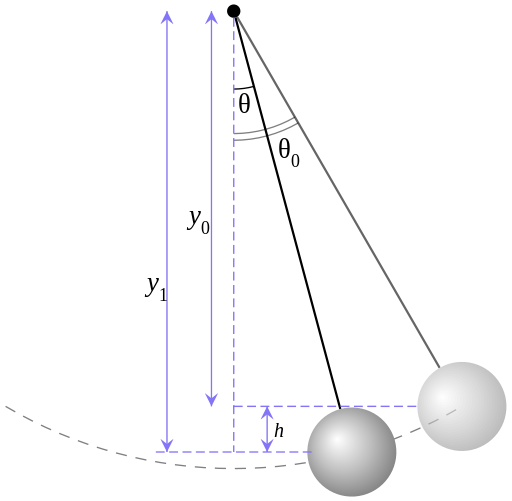
如之前的計算,
位能轉變:
動能轉變:
因為假設沒有能量流失,所以,在每一個角位移(
轉成用角位移來表示則為:
代入
為了解出這條方程,我嘗試用Matlab去計算。在網上一找,找到一條程式碼。它透過Matlab的ODE函數,找出
首先,先試試代入之前得出的結論,來驗證一下先前的計算結果。
代入初始角位移
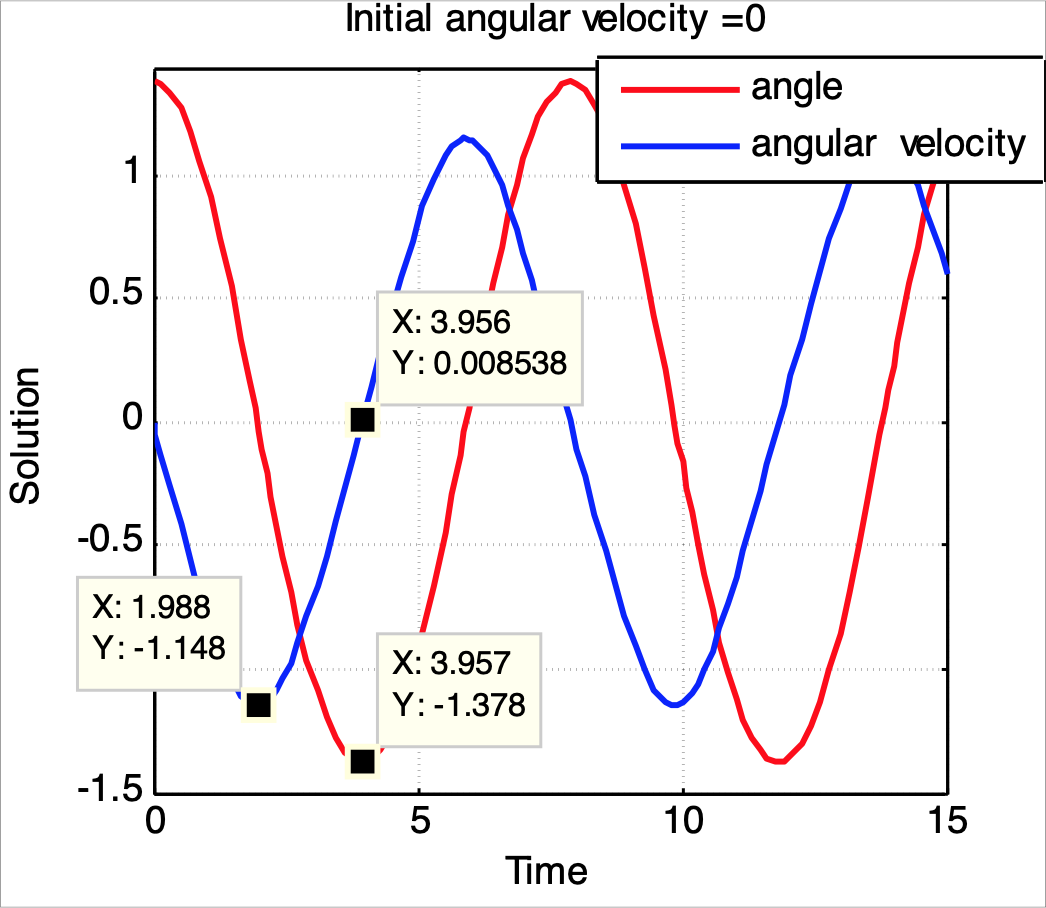
在上圖,x軸為時間,單位是s,而y軸分別為角位移和角速度。先看看紅線,當
好,現在來嘗試一下如果代入艾倫作拋體運動的情況。這時候艾倫水平前進的速度為馬匹在陸上行走的最高速度
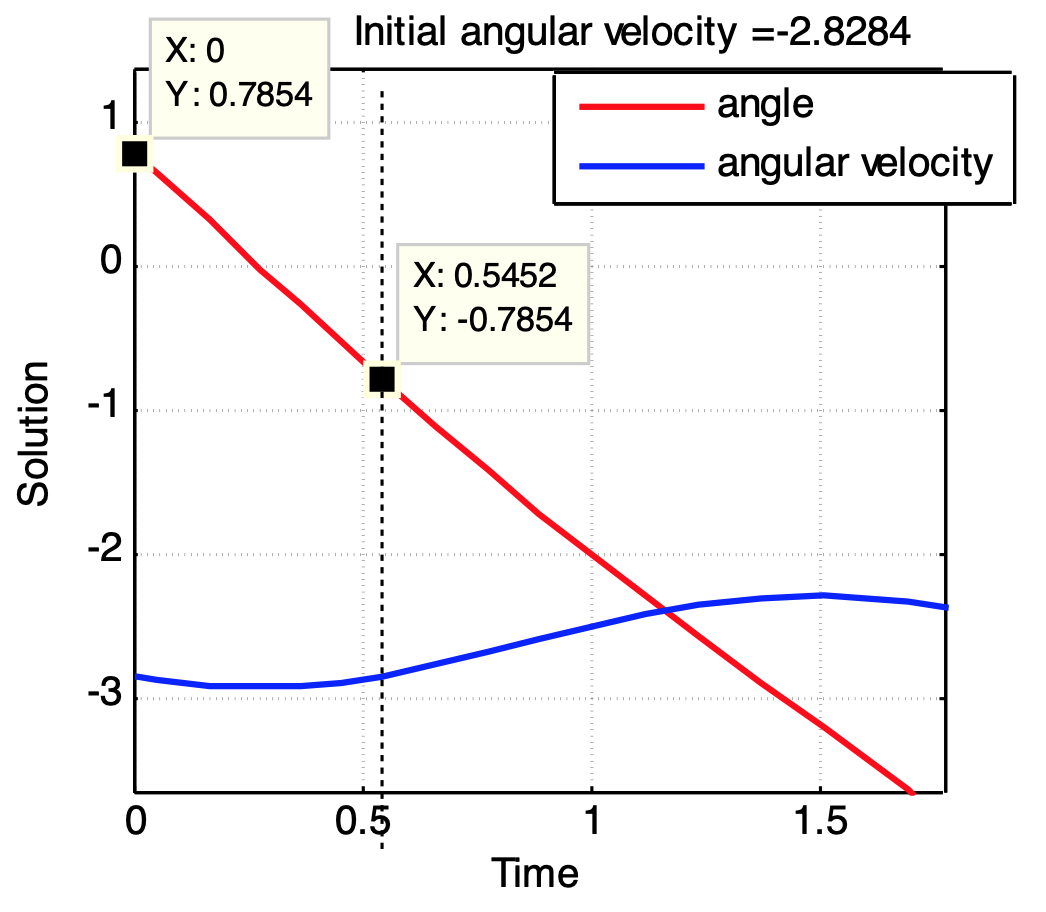
由上圖得出,在這個初速下,由
順帶一提,在這情況下,如果艾倫不在
省卻麻煩的鐘擺運動,簡化其為均速圓周運動去計算的話,那艾倫所受到繩索的拉力加速度為:
假設艾倫質量為
至底有6400牛頓有多大的力?想像一下,把艾倫的頭、手和腳牢牢的固定在天花板上,之後在艾倫腰間繫上一隻乳牛…我不敢說身體會斷開兩半,但我想必死無異吧…(順帶一提,【閒聊】人體承受立體機動裝置的加速度中,對於加速度的計算公式是有誤的,非均速圓周運動不能用
待續…
後記
寫這篇文章時,受到了空想科學系列的影響,那一段時間,都會十分科學地去計算要用多少時間才能把電熱水爐的水加熱、太陽透過窗戶,會為我房間上升多少度等問題。而這一篇則是啟發自【閒聊】人體承受立體機動裝置的加速度的研究,一開始是想驗算一下,但越看則越不對勁,覺得他有些地方錯了,於是用了一星期時間計算、編程和撰寫這文章,也算得上是有趣的回憶。
附錄
由於Matlab是要付費的,已經很久沒有使用過Matlab了,所以改用現在較為流行又免費的Python來完成。
311import numpy as np2from scipy.integrate import solve_ivp3import matplotlib.pyplot as plt4
5# Data of the problem.6g = 9.81 # gravitational acceleration7l = 12 # length of the pendulum (distance of the center of gravity from the suspension pivot)8
9# The second order equation of motion (ODE) was converted to first order form.10# This is the right hand side function. y[0] = angle, y[1] = angular velocity.11def f(t, y):12 return [y[1], -g/l*np.sin(y[0])]13
14thetadot0 = [-24/np.cos(np.pi/4)/12] # initial angular velocity15
16for td0 in thetadot0:17 Theta0 = [np.pi/4, td0] # initial condition: hanging down, with nonzero initial velocity18
19 # Solve the ODE20 sol = solve_ivp(f, [0, 2], Theta0, method='RK45', t_eval=np.linspace(0, 2, 1000))21
22 # Plot the solution23 plt.figure()24 plt.plot(sol.t, sol.y[0, :], linewidth=2, color='red', marker='none', label='angle')25 plt.plot(sol.t, sol.y[1, :], linewidth=2, color='blue', marker='none', label='angular velocity')26 plt.xlabel('Time')27 plt.ylabel('Solution')28 plt.title('Initial angular velocity = {}'.format(td0))29 plt.grid(True)30 plt.legend()31 plt.show()