數值方法入門:以單擺為例理解 Euler、RK2(midpoint)、RK4(classical)
關鍵信息密度高、一步到位。你之後回看,應該可以即刻上手。
0. 問題背景與符號
考慮常微分方程(ODE)初值問題:
當
1. 從 Taylor 展開到 Euler/RK
以 Taylor 展開:
Euler(顯式):只保留第一項
幾何上等於長方形積分;Local error
RK2(midpoint):取中點斜率
類似梯形/中點積分;Global error
RK4(classical):四點加權平均
幾何上=多點平均斜率;Global error
2. 單擺(Pendulum)作為非線性測試牀
模型(無阻尼)
2.1 矩陣(向量)更新式(Euler/RK2/RK4)
Euler:
RK2(Midpoint):
RK4(Classical)
以
2.2 真解(作對照)
單擺精確解可用 Jacobi 橢圓函數寫成(中大幅角時如此);小角近似
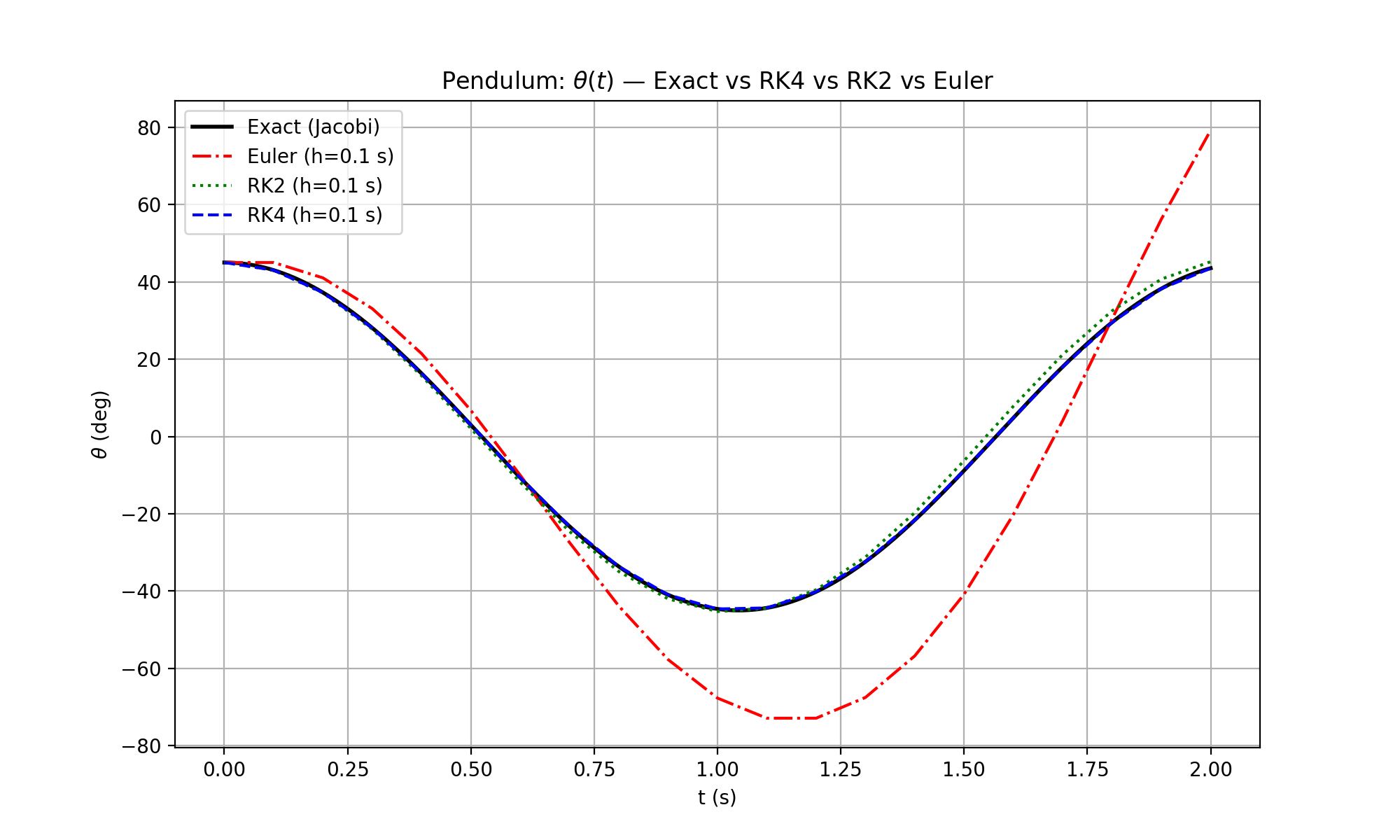
由上圖可見,如果h的值不夠細,即計算精度不夠高,在Euler算法上會嚴重偏移,但在RK4上還保持良好。
3. Gravity ODE:何時需要 RK?何時不需要?
恆定重力:
→ 這時 Euler 有
空氣阻力(加速度依賴
變重力場(例如
N-body 多體引力:無解析解,只能數值法(甚至要保結構積分器)
4. 輕量可重用工具:固定步長 Euler/RK2/RK4(Python)
我幫你寫咗通用整合器模組(最小但實用):
下載模組: ode_integrators.py
介面極簡:
xxxxxxxxxx21from ode_integrators import integrate2ts, ys = integrate(f, t0=0.0, y0=np.array([...]), t1=10.0, h=0.01, method="rk4")method可選"euler" | "rk2" | "rk4";固定步長h;回傳等距ts、配對ys。
4.1 範例 A:恆定重力(6 維)
xxxxxxxxxx121import numpy as np2from ode_integrators import integrate3
4g = 9.815def grav_rhs(t, y):6 # y = [x, y, z, vx, vy, vz]7 x, y_, z, vx, vy, vz = y8 ax, ay, az = 0.0, 0.0, -g9 return np.array([vx, vy, vz, ax, ay, az], dtype=float)10
11y0 = np.array([0, 0, 0, 10, 5, 20], dtype=float)12ts, ys = integrate(grav_rhs, t0=0.0, y0=y0, t1=2.0, h=0.1, method="rk2")4.2 範例 B:單擺(2 維)
xxxxxxxxxx131import numpy as np2from ode_integrators import integrate3
4g, L = 9.81, 1.05def pend_rhs(t, y):6 th, om = y7 return np.array([om, -(g/L)*np.sin(th)], dtype=float)8
9y0 = np.array([np.deg2rad(45.0), 0.0])10ts, ys = integrate(pend_rhs, 0.0, y0, 0.5, 0.05, method="rk4")11
12theta_deg = np.rad2deg(ys[:,0])13omega_deg_s = np.rad2deg(ys[:,1])想要事件偵測(撞地、過零交叉)、能量監控、或自動步長?請看下一節 SciPy。
5. 現成高階解算器:SciPy solve_ivp(自動步長/誤差控制)
如可用 SciPy,建議一般專案直接用 solve_ivp:
xxxxxxxxxx241import numpy as np2from scipy.integrate import solve_ivp3
4# 單擺例子5g, L = 9.81, 1.06def f(t, y):7 # y = [theta, omega]8 th, om = y9 return np.array([om, -(g/L)*np.sin(th)], dtype=float)10
11t_span = (0.0, 10.0)12y0 = np.array([np.deg2rad(45.0), 0.0], dtype=float)13
14# 常用顯式自適應:RK45(Dormand–Prince)15sol = solve_ivp(f, t_span, y0, method="RK45",16 rtol=1e-6, atol=1e-9, dense_output=True)17
18# 固定時間網格取樣19t_eval = np.linspace(0, 10, 501)20sol = solve_ivp(f, t_span, y0, method="RK45",21 t_eval=t_eval, rtol=1e-6, atol=1e-9)22
23ts = sol.t # (N,)24ys = sol.y.T # (N, d) 注意:SciPy 的 y 是 (d, N)方法選擇指引:
RK45:大多數非剛性問題的默認選擇DOP853:更高階顯式 RK(步數更省)Radau/BDF:剛性問題(隱式,穩定域大)rtol/atol:誤差控制旋鈕;越嚴格越慢但更準
Gravity 的建議
恆定重力:closed-form 或我上面的 rk2 已經夠;
變重力場/空阻/N-body:建議
RK45/DOP853;剛性時Radau/BDF。
6. 常見坑位 Checklist
步長是時間(秒),唔係角度或空間單位
單位一致(deg vs rad、m vs cm、N vs kN)
能量漂移:Euler 會嚴重漂移;RK2 好很多;RK4 更穩
剛性系統:顯式發散 → 試
Radau/BDF事件偵測:
solve_ivp的events可做(撞牆、過零)多體問題:注意數值穩定性與守恆(考慮 symplectic integrator)
附:可直接貼入你筆記的 SymPy 檢核程式(等價驗證&輸出 LaTeX)
xxxxxxxxxx521# SymPy: Pendulum ODE updates in matrix form + RK4 equivalence check2
3import sympy as sp4
5theta_n, omega_n, h, g, L = sp.symbols('theta_n omega_n h g L', real=True)6y_n = sp.Matrix([theta_n, omega_n])7
8def f(y):9 th, om = y10 return sp.Matrix([om, -(g/L) * sp.sin(th)])11
12# Euler13y_euler = sp.simplify(y_n + h * f(y_n))14
15# RK2 (midpoint)16k1_rk2 = f(y_n)17k2_rk2 = f(y_n + (h/2) * k1_rk2)18y_rk2 = sp.simplify(y_n + h * k2_rk2)19
20# RK4 (teaching form)21k1 = f(y_n)22k2 = f(y_n + (h/2) * k1)23k3 = f(y_n + (h/2) * k2)24k4 = f(y_n + h * k3)25y_rk4_A = sp.simplify(y_n + (h/6) * (k1 + 2*k2 + 2*k3 + k4))26
27# RK4 (long-form stages)28theta_1 = theta_n + (h/2)*k1[0]; omega_1 = omega_n + (h/2)*k1[1]29k2_alt = sp.Matrix([omega_1, -(g/L)*sp.sin(theta_1)])30
31theta_2 = theta_n + (h/2)*k2_alt[0]; omega_2 = omega_n + (h/2)*k2_alt[1]32k3_alt = sp.Matrix([omega_2, -(g/L)*sp.sin(theta_2)])33
34theta_3 = theta_n + h*k3_alt[0]; omega_3 = omega_n + h*k3_alt[1]35k4_alt = sp.Matrix([omega_3, -(g/L)*sp.sin(theta_3)])36
37y_rk4_B = sp.simplify(y_n + (h/6) * (k1 + 2*k2_alt + 2*k3_alt + k4_alt))38
39# Symbolic & numeric checks40print("Symbolic diff:")41sp.pprint(sp.simplify(y_rk4_A - y_rk4_B))42
43vals = {theta_n: 0.7, omega_n: -0.3, h: 0.05, g: 9.81, L: 1.2}44print("\nNumeric spot-check:", vals)45print("y_rk4_A =", sp.N(y_rk4_A.subs(vals)))46print("y_rk4_B =", sp.N(y_rk4_B.subs(vals)))47print("difference =", sp.N((y_rk4_A - y_rk4_B).subs(vals)))48
49# LaTeX blocks50print("\nLaTeX Euler:\n", sp.latex(y_euler))51print("\nLaTeX RK2:\n", sp.latex(y_rk2))52print("\nLaTeX RK4:\n", sp.latex(y_rk4_A))