Spacewar!

Spacewar!《太空戰爭！》是史帝芬·羅素與馬丁·格雷茨、韋恩·維塔寧、鮑勃·桑德斯、彼得·參孫等人於1962年合作開發的太空戰爭電子遊戲。初時，他們以麻省理工學院新安設的數碼裝置公司PDP-1迷你電腦作遊戲平台，並以PDP-1的匯編語言編寫代碼。後來，遊戲被學院其他學生和員工進一步擴展改良，當中包括丹·愛德華茲和彼得·參孫。程式設計師還把遊戲散佈至其他PDP-1電腦上，使它成為首款在單一機構以外可以接觸得到的遊戲。

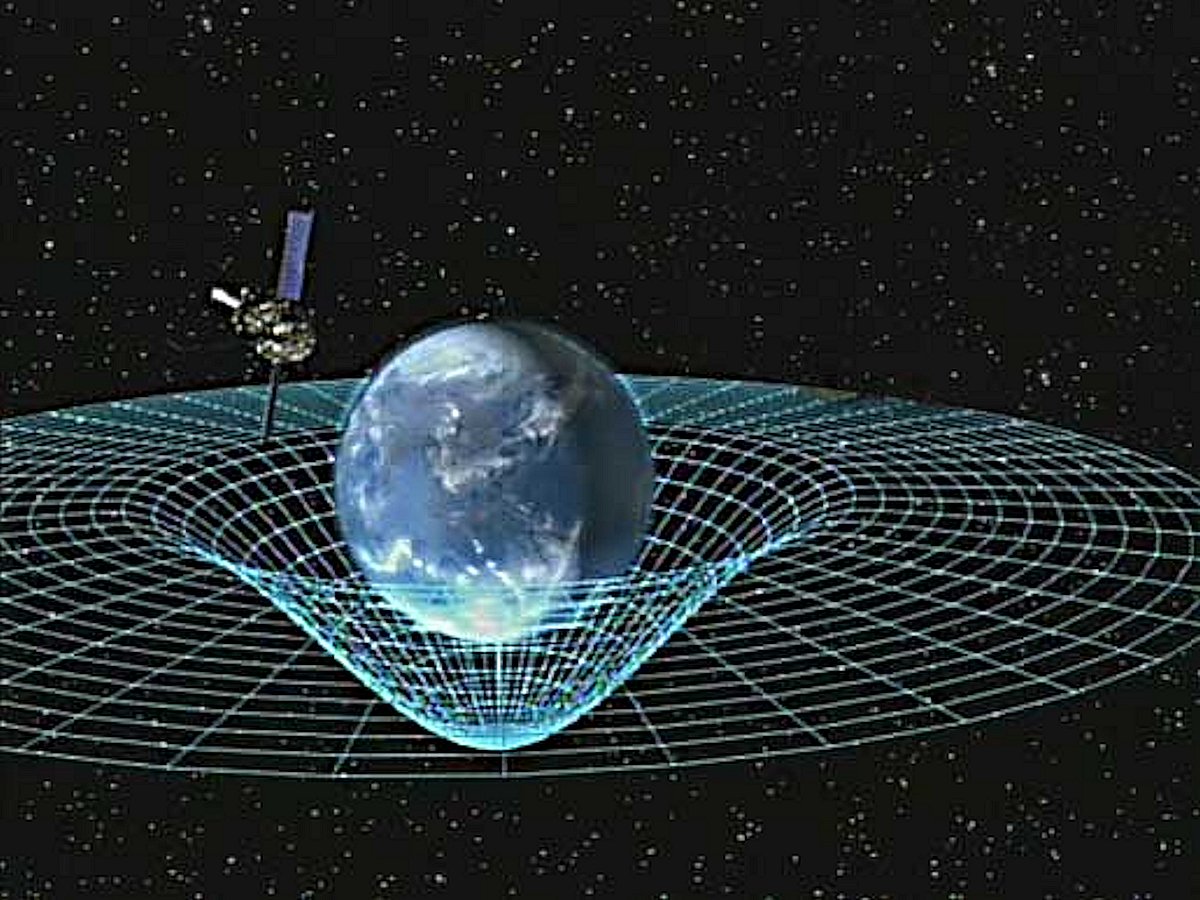
遊戲以星空為背景，兩名玩家須各自操作太空船「楔形船」或「針形船」，在恆星重力穴中移動並射擊對方船隻。每艘太空船都有有限的武器和燃料，即使玩家不加速，太空船仍會保持移動。玩家也可以在恆星附近航行以獲取重力助推。太空船只會在被魚雷擊中、兩船相撞或墜入恆星的情況下被摧毀。遊戲設有超空間跳躍功能，玩家可在任何時候使用，藉此隨機移動至熒幕上任一位置。但在某些版本中，每次使用這項功能都會增加太空船爆炸的風險。

0. 本章重點

1. 在遊戲中模擬物理中的引力，明白行星軌跡是怎樣運作

2. 因與上一章十分相似，本章會作為一個測驗，如果對內容有困惑，可以參考上一章節

1. 萬有引力¹

重力（英語：gravitation/gravity），是指具有質量的物體之間相互吸引的作用，也是物體重量的來源。在1687年，艾薩克·牛頓在他的《自然哲學的數學原理》一書中發表了萬有引力定律。

如果兩個質點的質量分別為$m_1$$m_1$和$m_2$$m_2$，並且它們之間的距離為$r$$r$，則它們之間的引力$F$$F$為:

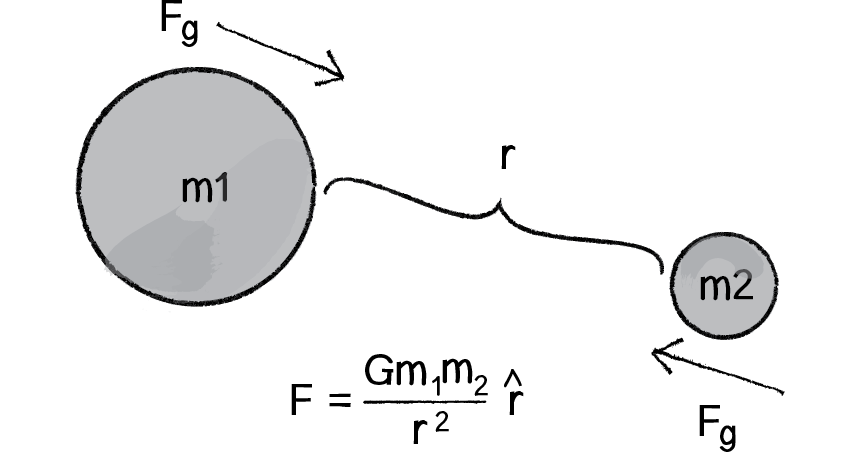
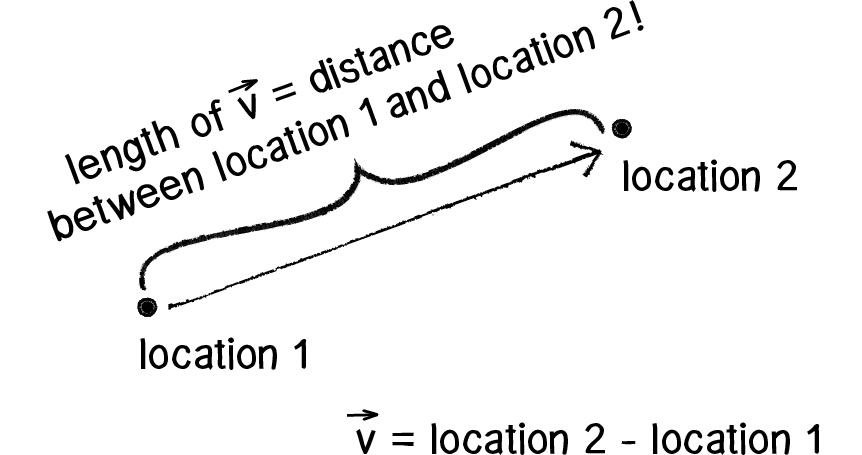
1.1 用程式實現

​x
1
m1 = 1000
2
m2 = 1e6
3
object1Pos = PVector(0,0)
4
object2Pos = PVector(0,0)
5
object1Vec = PVector(0,0)
6
object2Vec = PVector(0,0)
7
G = 6.67E-6 #just a random number, not the same as physics
8

9
def setup():
10
    global object1Pos, object2Pos
11
    size(600,600)
12
    object1Pos = PVector(random(0, width), random(0, height))
13
    object2Pos = PVector(width/2, height/2)
14
    
15
def draw():
16
    global object1Pos, object2Pos, object1Vec, object2Vec
17
    background(50)
18
    
19
    r = PVector.sub(object2Pos, object1Pos)
20
    F = PVector.mult(r.copy().normalize(), G*m1*m2/sq(r.mag()))
21
    
22
    object1Vec = PVector.add(object1Vec, F)
23
    object1Pos = PVector.add(object1Pos, object1Vec)
24
    
25
    fill('#FFFF00')
26
    ellipse(object1Pos.x, object1Pos.y, 50,50)
27
    fill(0)
28
    ellipse(object2Pos.x, object2Pos.y, 50,50)

1.2 轉用class去管理

star.pyde

xxxxxxxxxx
25
1
from star import *
2

3
star1 = star2 = 0
4
G = 6.67E-6  #just a random number, not the same as physics
5

6
def setup():
7
    global star1, star2
8
    size(600,600)
9
    star1 = Star(1000, PVector(width/2, height/4))
10
    star2 = Star(1e6, PVector(width/2, height/2))
11
    
12
def draw():
13
    global star1, star2
14

15
    background(50)
16
    
17
    r = PVector.sub(star2.pos, star1.pos)
18
    F = PVector.mult(r.copy().normalize(), G*star1.mass*star2.mass/sq(r.mag()))
19
    
20
    star1.applyForce(F)
21
    
22
    fill('#FFFF00')
23
    ellipse(star1.pos.x, star1.pos.y, 50,50)
24
    fill(0)
25
    ellipse(star2.pos.x, star2.pos.y, 50,50)

star.py

xxxxxxxxxx
9
1
class Star(object):
2
    def __init__(self, _mass, _pos):
3
        self.mass = _mass
4
        self.pos = _pos
5
        self.vec = PVector()
6

7
    def applyForce(self, _force):
8
        self.vec = PVector.add(self.vec, _force)
9
        self.pos = PVector.add(self.pos , self.vec)

效果跟之前是一樣的，只是轉了用class的方法去做，而且star1一開始出現的地方也固定了方便觀察，內容都是一樣的。

1.3 行星是怎樣轉轉的?

只要將star1加入一點點初速，你就會見到完全不一樣的效果。

star.pyde

xxxxxxxxxx
28
1
from star import *
2

3
star1 = star2 = 0
4
G = 6.67E-6
5

6
def setup():
7
    
8
    global star1, star2
9
    size(600,600)
10
    star1 = Star(1000, PVector(width/2, height/4))
11
    star1.vec = PVector(4, 0)
12
    star2 = Star(1e6, PVector(width/2, height/2))
13

14
def draw():
15
    global star1, star2
16

17
    fill(50, 50, 50, 1)
18
    rect(0, 0 ,width, height)
19
    
20
    r = PVector.sub(star2.pos, star1.pos)
21
    F = PVector.mult(r.copy().normalize(), G*star1.mass*star2.mass/sq(r.mag()))
22
    
23
    star1.applyForce(F)
24
    
25
    fill('#FFFF00')
26
    ellipse(star1.pos.x, star1.pos.y, 50,50)
27
    fill(0)
28
    ellipse(star2.pos.x, star2.pos.y, 50,50)

上面這四張圖，star1.vec的初始值分別是 PVector(4, 0), PVector(5, 0), PVector(7, 0), PVector(8, 0)，大於8的話，中間的star2便不能夠吸引star1圍繞著轉。

中文學校的初中物理課程就會認識到一個定律叫開普勒定律。其主要內容就是透過觀察發現到， 行星軌道不是圓形而是橢圓形，而且行星公轉的速度不是均速而是時快時慢。這些論點，大大地動搖了當時的天文學與物理學。

一個世紀後，牛頓應用他的第二定律和萬有引力定律，在數學上嚴格地証明了開普勒定律，也讓人了解了其中的物理意義。

透過數學公式去計算的話，會涉及到複雜的微分方程，難以向初中生解釋。

但，現在你可以透過自己寫的幾行程式，親自驗算天體軌跡是如何運行和形成的。

至於其他遊戲的部分，幾乎跟上一章是完全一樣的，可以用上一章的內容來修改。