Minimax 演算法

Minimax 演算法0. recursion 遞歸1. 為遊戲加入打和2. 加入random AI跟玩家對玩3. 加入dummy AI4. 加入minimax演算法5. 令AI懂得阻擋我方6. 既能阻擋我方，又懂得贏7. 令分數與depth成關係

0. recursion 遞歸

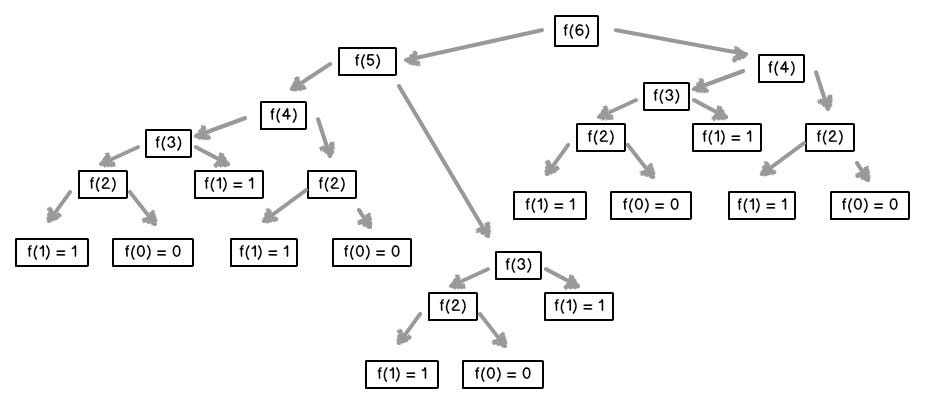
Fibonacci sequence(費波那契數)是一個常見用來解釋recursion遞歸概念的數列。定義上，

\begin{matrix} (1) & \begin{matrix} F_{0} = 0 \\ F_{1} = 1 \\ F_{n} = F_{n - 1} + F_{n - 2} (n ⩾ 2) \end{matrix} \end{matrix}

用文字來說，就是斐波那契數列由0和1開始，之後的費波那契數就是由之前的兩數相加而得出。首幾個費波那契數是：

1、 1、 2、 3、 5、 8、 13、 21、 34、 55、 89、 144、 233、 377、 610、 987……


1
def setup():
2
    for i in range(1,10):
3
        print(Fibonacci(i))
4
    exit()
5
    
6
def Fibonacci(n):
7
    if n == 0:
8
        return 0
9
    if n == 1:
10
        return 1
11
    if n >=2:
12
        return Fibonacci(n-1)+Fibonacci(n-2)

得出結果:

這個在函數之中call自己的方法叫做遞歸recursion，遞歸在程式中非常常用，但不一定時好方法。

以上述的斐波那契數列為例，


xxxxxxxxxx
5
1
def setup():
2
    timer = millis()
3
    print(Fibonacci(10))
4
    print(millis()-timer)
5
    exit()

$F_{10}$ $F_{20}$ $F_{20}$ $F_{19}$ $F_{18}$ $F_{19}$ $F_{18}$ $F_{18}$ $F_{17}$ $F_{16}$ ，如此類推，其實有很多重覆了的計算，會令程式以幾何級的時間遞增。

1. 為遊戲加入打和

connectFour_AI.pyde:


x
1
from spot import *
2
from gameBoard import *
3

4
gameBoard = 0
5

6
def setup():
7
    global grids, gameBoard
8

9
    size(700, 600)
10
    ellipseMode(CENTER)
11
    frameRate(10)
12
    gameBoard = GameBoard()
13

14
def draw():
15
    background(200)
16
    gameBoard.display() 
17

18
def mousePressed():
19
    global gameBoard
20
    for i in range(7):
21
        if (mouseX > width/7*i and mouseX < width/7*(i+1)):
22
            gameBoard.trigger(i)

gameBoard.py:


xxxxxxxxxx
90
1
from spot import *
2

3
class GameBoard(object):
4

5
    def __init__(self):
6
        self.grids = []
7
        for i in range(6):
8
            temp = []
9
            for j in range(7):
10
                temp.append(Spot(i, j, width/7*(j+.5), height/6*(i+.5), ''))
11
            self.grids.append(temp)
12
        self.currentRow = 0
13
        self.currentCol = 0
14
        self.colHeight = [0, 0, 0, 0, 0, 0, 0]
15
        self.currentPlayer = 'R'
16
        self.gameOver = False
17
        self.winner = None
18

19
    def display(self):
20
        for i in range(6):
21
                for j in range(7):
22
                    self.grids[i][j].display()
23
        if self.gameOver == True:            
24
            textAlign(CENTER, CENTER)
25
            textSize(100)
26
            fill('#0000FF')
27
            if self.winner == 'R':
28
                text('YOU WIN!!!!', width/2, height/2)
29
            elif self.winner == 'Y':
30
                text('GAME OVER', width/2, height/2)
31
            elif self.winner == 'O':
32
                text('TIE', width/2, height/2)
33
            
34
    def swapPlayer(self):
35
        if self.currentPlayer == 'R':
36
            self.currentPlayer = 'Y'
37
        elif self.currentPlayer == 'Y':
38
            self.currentPlayer = 'R'
39

40
    def trigger(self, i):
41
        if self.gameOver == False:
42
            if self.colHeight[i] < 6:
43
                self.colHeight[i] += 1
44
                self.currentCol = i
45
                self.currentRow = 6 - self.colHeight[i]
46
                self.grids[self.currentRow][self.currentCol].value = self.currentPlayer
47
                self.winner = self.checkWin()
48
                if self.winner != None:
49
                    self.gameOver = True
50
                    return
51
                self.swapPlayer()
52
                
53
    def checkWin(self):
54
        gs = self.grids
55

56
        # check horizontal
57
        for i in range(6):
58
            for j in range(4):
59
                if gs[i][j].value == gs[i][j+1].value == gs[i][j+2].value == gs[i][j+3].value\
60
                        and gs[i][j].value != '':
61
                    return gs[i][j].value
62

63
        # check vertical
64
        for i in range(3):
65
            for j in range(7):
66
                if gs[i][j].value == gs[i+1][j].value == gs[i+2][j].value == gs[i+3][j].value\
67
                        and gs[i][j].value != '':
68
                    return gs[i][j].value
69

70
        # check right cross
71
        for i in range(3):
72
            for j in range(4):
73
                if gs[i][j].value == gs[i+1][j+1].value == gs[i+2][j+2].value == gs[i+3][j+3].value\
74
                        and gs[i][j].value != '':
75
                    return gs[i][j].value
76

77
        # check left cross
78
        for i in range(3):
79
            for j in range(3, 7):
80
                if gs[i][j].value == gs[i+1][j-1].value == gs[i+2][j-2].value == gs[i+3][j-3].value\
81
                        and gs[i][j].value != '':
82
                    return gs[i][j].value
83
                
84
        # if all the grids are filled, the game is tie
85
        isAllNull = False
86
        for i in range(6):
87
            for j in range(7):
88
                isAllNull = isAllNull or gs[i][j].value == ''
89
        if isAllNull == False:
90
            return 'O'

spot.py:


xxxxxxxxxx
21
1
class Spot(object):
2
    def __init__(self, _i, _j, _x, _y, _value):
3
        self.i = _i
4
        self.j = _j
5
        self.x = _x
6
        self.y = _y
7
        self.value = ''
8

9
    def display(self):
10
        stroke('#000000')
11
        strokeWeight(2)
12
        fill(self.matchColor(self.value))
13
        ellipse(self.x, self.y, 80, 80)
14

15
    def matchColor(self, _value):
16
        if _value == '':
17
            return '#FFFFFF'
18
        elif _value == 'R':
19
            return '#FF5641'
20
        elif _value == 'Y':
21
            return '#FFDF37'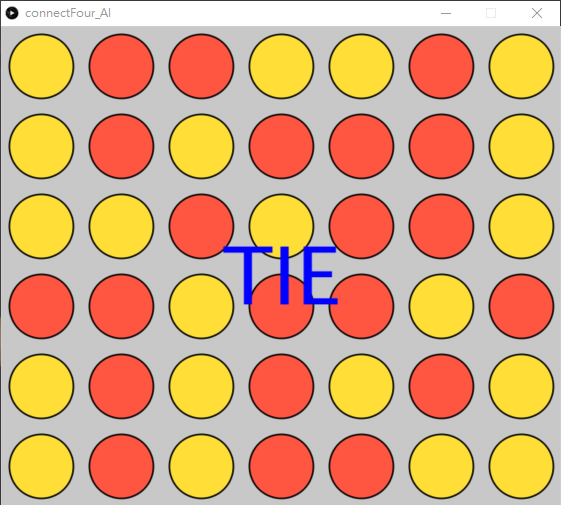

首先在gameBoard.py的class中，


xxxxxxxxxx
11
1
 def checkWin(self):
2
        gs = self.grids
3
        #other cods
4
                
5
        # if all the grids are filled, the game is tie
6
        isAllNull = False
7
        for i in range(6):
8
            for j in range(7):
9
                isAllNull = isAllNull or gs[i][j].value == ''
10
        if isAllNull == False:
11
            return 'O'

在checkWin()的最後加入isAllNull = False，之後對每一個格都做or運算，只要其中一個格是沒有填的話，isAllNull都會變成True，只有在全部都填滿下，isAllNull才會運算完42次後都是False，如果是False的話，即全部格已滿，所以就是打和了。


xxxxxxxxxx
8
1
def display(self):
2
       #other cods
3
        if self.winner == 'R':
4
            text('YOU WIN!!!!', width/2, height/2)
5
        elif self.winner == 'Y':
6
            text('GAME OVER', width/2, height/2)
7
        elif self.winner == 'O':
8
            text('TIE', width/2, height/2)

之後同樣是在gameBoard.py中，如果self.winner == 'O'，即遊戲打和，則在顯示中加入打和。

2. 加入random AI跟玩家對玩

connectFour_AI.pyde:


xxxxxxxxxx
28
1
from spot import *
2
from gameBoard import *
3

4
gameBoard = 0
5

6

7
def setup():
8
    global grids, gameBoard
9

10
    size(700, 600)
11
    ellipseMode(CENTER)
12
    frameRate(10)
13

14
    gameBoard = GameBoard()
15

16

17
def draw():
18
    background(200)
19
    gameBoard.display()
20
   
21

22
def mousePressed():
23
    global gameBoard
24
    for i in range(7):
25
        if (mouseX > width/7*i and mouseX < width/7*(i+1)):
26
            gameBoard.trigger(i)
27
            if gameBoard.currentPlayer == 'Y':
28
                    gameBoard.brain.autoPlay()

gameBoard.py


xxxxxxxxxx
95
1
from spot import *
2
from AIBrain import *
3

4
class GameBoard(object):
5

6
    def __init__(self):
7
        self.grids = []
8
        for i in range(6):
9
            temp = []
10
            for j in range(7):
11
                temp.append(Spot(i, j, width/7*(j+.5), height/6*(i+.5), ''))
12
            self.grids.append(temp)
13

14
        self.currentRow = 0
15
        self.currentCol = 0
16
        self.colHeight = [0, 0, 0, 0, 0, 0, 0]
17
        self.currentPlayer = 'R'
18
        self.gameOver = False
19
        self.winner = None
20
        self.brain = aiBrain(self)
21

22
    def display(self):
23
        for i in range(6):
24
                for j in range(7):
25
                    self.grids[i][j].display()
26
        if self.gameOver == True:            
27
            textAlign(CENTER, CENTER)
28
            textSize(100)
29
            fill('#0000FF')
30
            if self.winner == 'R':
31
                text('YOU WIN!!!!', width/2, height/2)
32
            elif self.winner == 'Y':
33
                text('GAME OVER', width/2, height/2)
34
            elif self.winner == 'O':
35
                text('TIE', width/2, height/2)
36
            
37

38
    def swapPlayer(self):
39
        if self.currentPlayer == 'R':
40
            self.currentPlayer = 'Y'
41
        elif self.currentPlayer == 'Y':
42
            self.currentPlayer = 'R'
43

44
    def trigger(self, i):
45
        if self.gameOver == False:
46
            if self.colHeight[i] < 6:
47
                self.colHeight[i] += 1
48
                self.currentCol = i
49
                self.currentRow = 6 - self.colHeight[i]
50
                self.grids[self.currentRow][self.currentCol].value = self.currentPlayer
51
                self.winner = self.checkWin()
52
                if self.winner != None:
53
                    self.gameOver = True
54
                    return
55
                self.swapPlayer()
56
                
57

58
    def checkWin(self):
59
        gs = self.grids
60

61
        # check horizontal
62
        for i in range(6):
63
            for j in range(4):
64
                if gs[i][j].value == gs[i][j+1].value == gs[i][j+2].value == gs[i][j+3].value\
65
                        and gs[i][j].value != '':
66
                    return gs[i][j].value
67

68
        # check vertical
69
        for i in range(3):
70
            for j in range(7):
71
                if gs[i][j].value == gs[i+1][j].value == gs[i+2][j].value == gs[i+3][j].value\
72
                        and gs[i][j].value != '':
73
                    return gs[i][j].value
74

75
        # check right cross
76
        for i in range(3):
77
            for j in range(4):
78
                if gs[i][j].value == gs[i+1][j+1].value == gs[i+2][j+2].value == gs[i+3][j+3].value\
79
                        and gs[i][j].value != '':
80
                    return gs[i][j].value
81

82
        # check left cross
83
        for i in range(3):
84
            for j in range(3, 7):
85
                if gs[i][j].value == gs[i+1][j-1].value == gs[i+2][j-2].value == gs[i+3][j-3].value\
86
                        and gs[i][j].value != '':
87
                    return gs[i][j].value
88
                
89
        # if all the grids are filled, the game is tie
90
        isAllNull = False
91
        for i in range(6):
92
            for j in range(7):
93
                isAllNull = isAllNull or gs[i][j].value == ''
94
        if isAllNull == False:
95
            return 'O'

AIBrain.py:


xxxxxxxxxx
29
1
import copy
2
import random
3

4

5
class aiBrain(object):
6

7
    def __init__(self, _gameBoard):
8
        self.gameBoard = _gameBoard
9

10
    def autoPlay(self):
11
        bestScore = float('-inf')
12

13
        # fill the available colume to an list
14
        availableCol = []
15
        for j in range(7):
16
            if self.gameBoard.grids[0][j].value == '':
17
                availableCol.append(j)
18
        # shuffle the list
19
        random.shuffle(availableCol)
20

21
        for move in availableCol:
22
            score = self.minimax(self.gameBoard, 4, False)
23
            if (score > bestScore):
24
                bestScore = score
25
                bestMove = move
26
        self.gameBoard.trigger(bestMove)
27

28
    def minimax(self, _gameBoard, _depth, _isMaximizing):
29
        return 1

加入一個叫AIBrain.py的檔案，這個檔案一開始先做一點簡單的測試。在初始化時，匯入現有的gameBoard


xxxxxxxxxx
4
1
class aiBrain(object):
2

3
    def __init__(self, _gameBoard):
4
        self.gameBoard = _gameBoard

之後，


xxxxxxxxxx
20
1
 def autoPlay(self):
2
        bestScore = float('-inf')
3

4
        # //fill the available colume to an list
5
        availableCol = []
6
        for j in range(7):
7
            if self.gameBoard.grids[0][j].value == '':
8
                availableCol.append(j)
9
        # shuffle the list
10
        random.shuffle(availableCol)
11

12
        for move in availableCol:
13
            score = self.minimax(self.gameBoard, 4, False)
14
            if (score > bestScore):
15
                bestScore = score
16
                bestMove = move
17
        self.gameBoard.trigger(bestMove)
18

19
    def minimax(self, _gameBoard, _depth, _isMaximizing):
20
        return 1

我們要為下一步所有可能的步數去計分，才知那一個才對AI方最有利。

我們設定玩家方為正分，AI方為負分數，所以每一步越是負得多，即對AI方是最有利的。

一開始設定bestScore = float('-inf')，就是負無限大。

將一個叫availableCol = []去裝起所有可能的下一步，這7個欄之中，如果if self.gameBoard.grids[0][j].value == '':即最上一格為空，即可以填入，所以就將其append到availableCol。

下一步是shuffle即調亂整個列，如果分數是相同的話，則最後結果會有亂數，不會每次都是由左至右。

之後每一個可能的落祺步，都加入一個叫minimax()的演算法去幫這一步計分，分數最大的步就是最佳答案，於是我們便落子這一步。但現階段我們的minimax()演算法暫時甚麼都沒有，全部回傳的分數都是1，我們先試一試這個思路是否行得通。

3. 加入dummy AI

AIBrain.py:


xxxxxxxxxx
45
1
import copy
2
import random
3

4

5
class aiBrain(object):
6

7
    def __init__(self, _gameBoard):
8
        self.gameBoard = _gameBoard
9

10
    def autoPlay(self):
11
        bestScore = float('-inf')
12
        bestMove = random.randint(0, 5)  # the range is a, b+1
13

14
        # //fill the available colume to an list
15
        availableCol = []
16
        for j in range(7):
17
            if self.gameBoard.grids[0][j].value == '':
18
                availableCol.append(j)
19
        # shuffle the list
20
        random.shuffle(availableCol)
21

22
        for move in availableCol:
23
            possibleBoard = copy.deepcopy(self.gameBoard)
24
            possibleBoard.trigger(move)
25
            score = self.minimax(possibleBoard, 4, False)
26
            print(move, score)
27
            if (score > bestScore):
28
                bestScore = score
29
                bestMove = move
30
            print(bestMove)
31
        print('')
32
        self.gameBoard.trigger(bestMove)
33

34
    def score(self, _winner):
35
        if _winner == 'R':
36
            return 10
37
        elif _winner == 'Y':
38
            return -10
39
        elif _winner == 'O':
40
            return 0
41

42
    def minimax(self, _gameBoard, _depth, _isMaximizing):
43
        winner = _gameBoard.checkWin()
44
        if winner != None:
45
            return self.score(winner)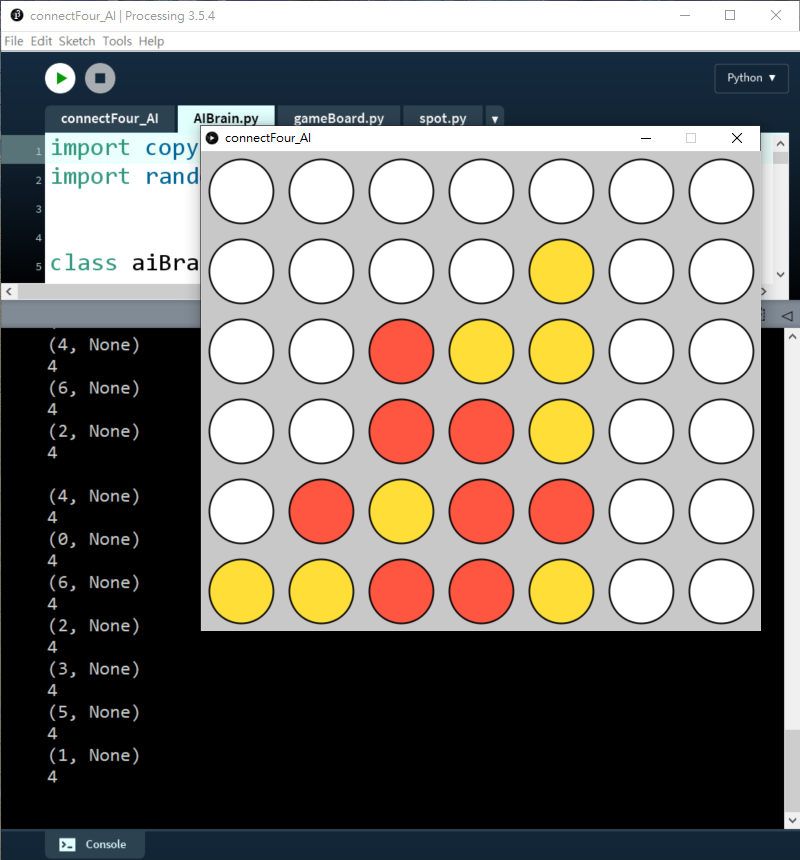

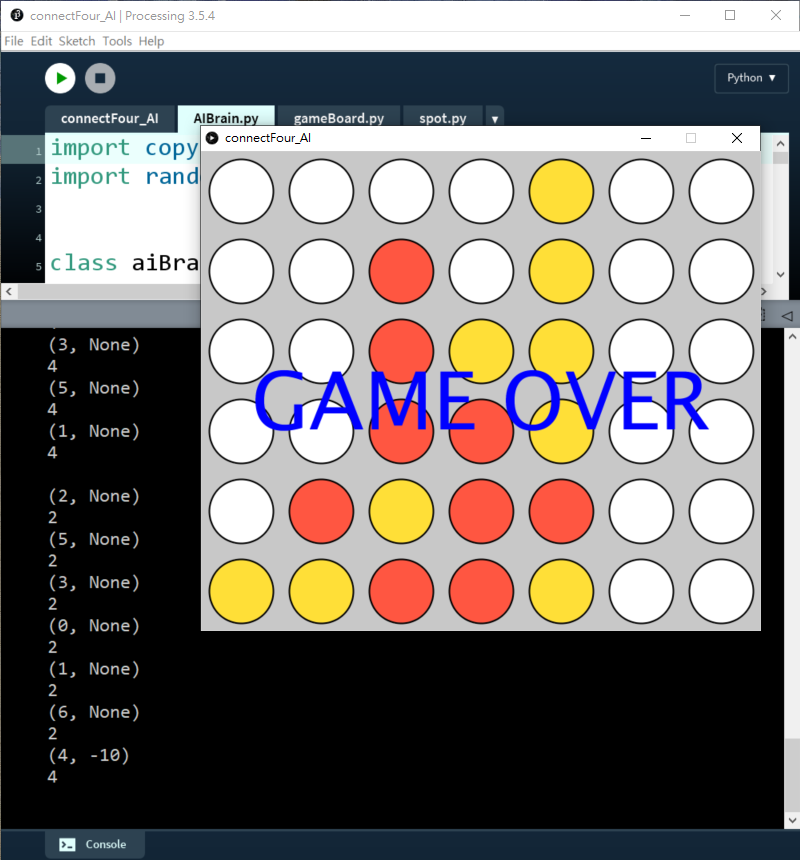
在AIBrain.py中，


xxxxxxxxxx
11
1
    for move in availableCol:
2
        possibleBoard = copy.deepcopy(self.gameBoard)
3
        possibleBoard.trigger(move)
4
        score = self.minimax(possibleBoard, 4, False)
5
        print(move, score)
6
        if (score > bestScore):
7
            bestScore = score
8
            bestMove = move
9
        print(bestMove)
10
    print('')
11
    self.gameBoard.trigger(bestMove)

我們用copy.deepcopy()去將整個gameboard複製。Python和其他高級語言一樣，如果只用=去複製一個class的話，只會複製其id，之後修改這個class的話，被複製的和複製後的class都會改變，所以要用copy.deepcopy()去將整個gameboard完全複製。

之後就將當前這一步落子到複製出來的possibleBoard，接著就將這個gameboard放到minimax演算法中提出最佳答案。


xxxxxxxxxx
4
1
    def minimax(self, _gameBoard, _depth, _isMaximizing):
2
        winner = _gameBoard.checkWin()
3
        if winner != None:
4
            return self.score(winner)

上一步我們的minimax演算法只會回傳1分出來，甚麼功能也沒有的。這一步我們幫輸入的gameboard檢查一下有否贏、輸或打和，分別根據這3個情況打分如下:


xxxxxxxxxx
7
1
    def score(self, _winner):
2
        if _winner == 'R':
3
            return 10
4
        elif _winner == 'Y':
5
            return -10
6
        elif _winner == 'O':
7
            return 0

贏出的話就打10分，輸就是-10分，打和就是0分。

由於設定了bestScore最開始時是負無限大，所以即使AI(黃色棋子)輸出的話是-10分，也依然大於負無限大，所以這個dummy AI都會落子，但只限於此。這個AI唯一的功能是如果下一步AI會贏，而玩家又沒有阻擋的話，AI就會懂得落子去贏出遊戲，但這個AI既不懂阻擋玩家，更不會佈局的。

4. 加入minimax演算法


xxxxxxxxxx
79
1
import copy
2
import random
3

4

5
class aiBrain(object):
6

7
    def __init__(self, _gameBoard):
8
        self.gameBoard = _gameBoard
9

10
    def autoPlay(self):
11
        bestScore = float('-inf')
12
        bestMove = random.randint(0, 5)  # the range is a, b+1
13

14
        # //fill the available colume to an list
15
        availableCol = []
16
        for j in range(7):
17
            if self.gameBoard.grids[0][j].value == '':
18
                availableCol.append(j)
19
        # shuffle the list
20
        random.shuffle(availableCol)
21

22
        for move in availableCol:
23
            possibleBoard = copy.deepcopy(self.gameBoard)
24
            possibleBoard.trigger(move)
25
            score = self.minimax(possibleBoard, 1, False)
26
            print(move, score)
27
            if (score > bestScore):
28
                bestScore = score
29
                bestMove = move
30
            print(bestMove)
31
        print('')
32
        self.gameBoard.trigger(bestMove)
33

34
    def score(self, _winner):
35
        if _winner == 'R':
36
            return 10
37
        elif _winner == 'Y':
38
            return -10
39
        elif _winner == 'O':
40
            return 0
41

42
    def minimax(self, _gameBoard, _depth, _isMaximizing):
43
        winner = _gameBoard.checkWin()
44
        if winner != None or _depth == 0:
45
            return self.score(winner)
46

47
        if _isMaximizing:
48
            bestScore = float('-inf')
49
            # //fill the available colume to an list
50
            availableCol = []
51
            for j in range(7):
52
                if _gameBoard.grids[0][j].value == '':
53
                    availableCol.append(j)
54
            # shuffle the list
55
            random.shuffle(availableCol)
56

57
            for move in availableCol:
58
                possibleBoard = copy.deepcopy(_gameBoard)
59
                possibleBoard.trigger(move)
60
                score = self.minimax(possibleBoard, _depth - 1, False)
61
                bestScore = max(score, bestScore)
62
            return bestScore
63

64
        else:
65
            bestScore = float('inf')
66
            # //fill the available colume to an list
67
            availableCol = []
68
            for j in range(7):
69
                if _gameBoard.grids[0][j].value == '':
70
                    availableCol.append(j)
71
            # shuffle the list
72
            random.shuffle(availableCol)
73

74
            for move in availableCol:
75
                possibleBoard = copy.deepcopy(_gameBoard)
76
                possibleBoard.trigger(move)
77
                score = self.minimax(possibleBoard, _depth - 1, True)
78
                bestScore = min(score, bestScore)
79
            return bestScore

測試depth = 1:

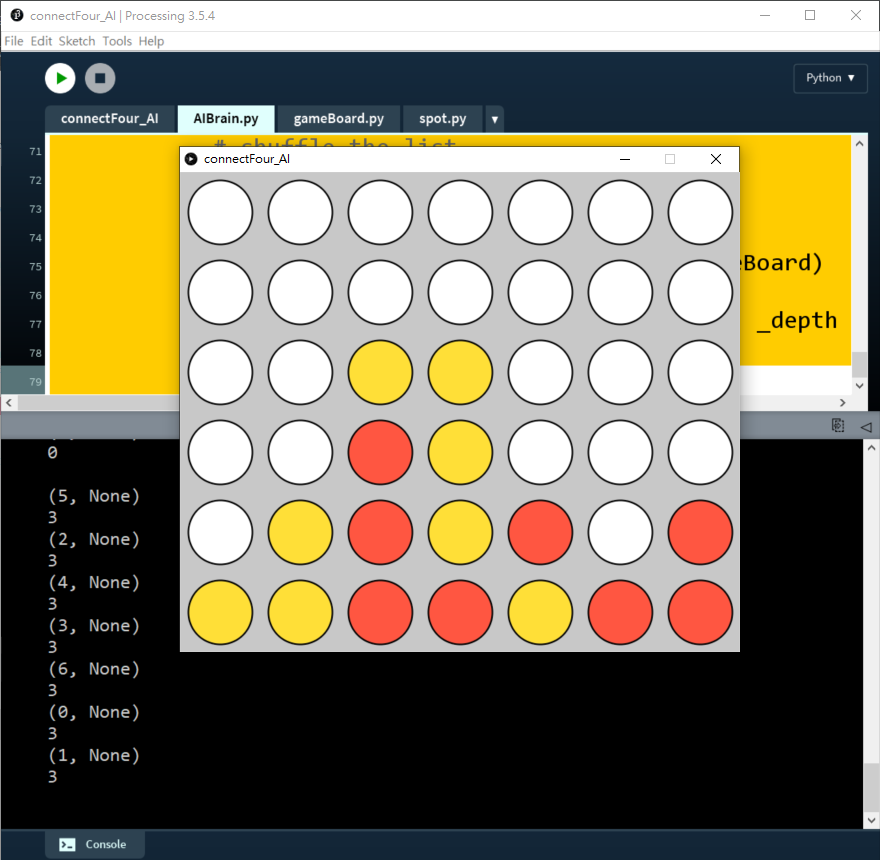
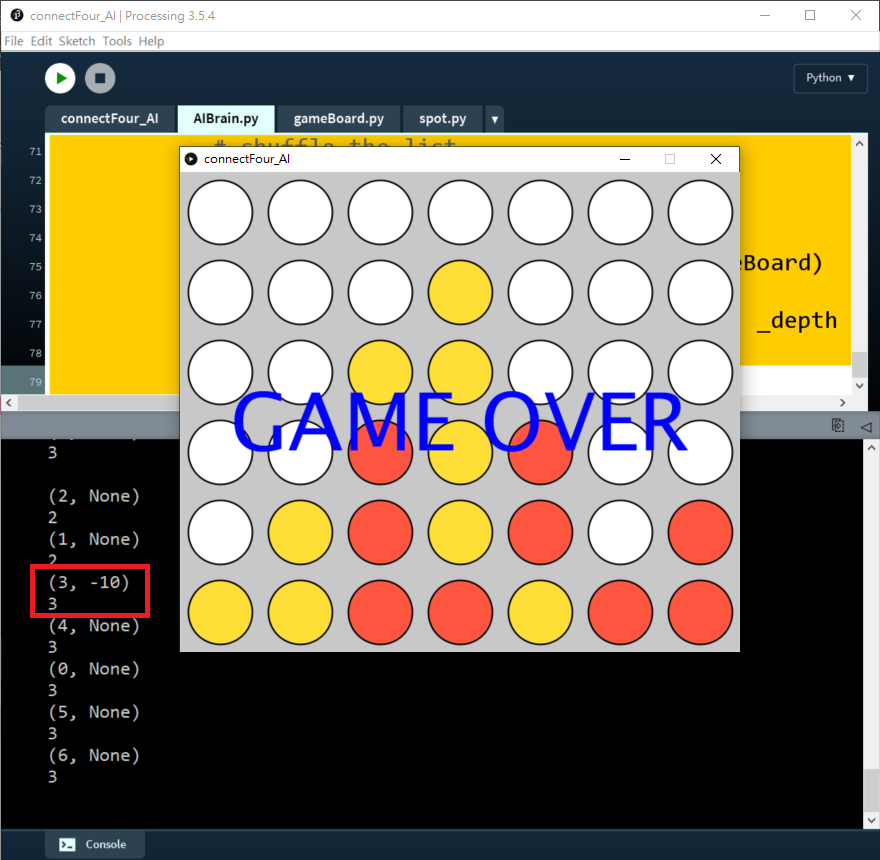
測試depth = 2:

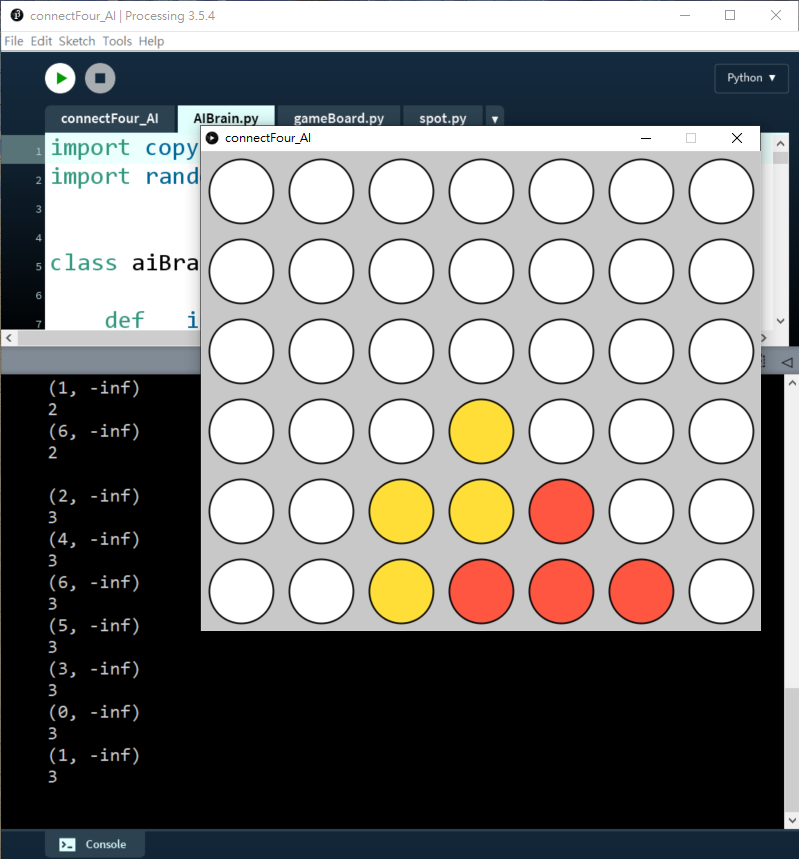
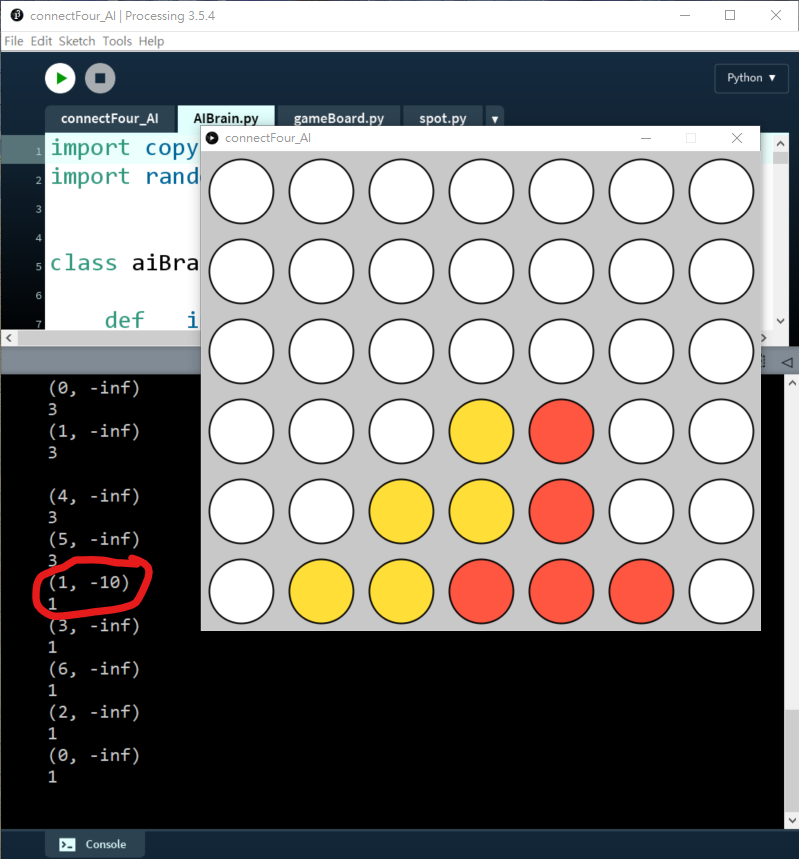
效果：即使depth再增加，AI都只會懂得幫自己提早抬轎，而不懂阻擋我。


xxxxxxxxxx
38
1
 def minimax(self, _gameBoard, _depth, _isMaximizing):
2
        winner = _gameBoard.checkWin()
3
        if winner != None or _depth == 0:
4
            return self.score(winner)
5

6
        if _isMaximizing:
7
            bestScore = float('-inf')
8
            # //fill the available colume to an list
9
            availableCol = []
10
            for j in range(7):
11
                if _gameBoard.grids[0][j].value == '':
12
                    availableCol.append(j)
13
            # shuffle the list
14
            random.shuffle(availableCol)
15

16
            for move in availableCol:
17
                possibleBoard = copy.deepcopy(_gameBoard)
18
                possibleBoard.trigger(move)
19
                score = self.minimax(possibleBoard, _depth - 1, False)
20
                bestScore = max(score, bestScore)
21
            return bestScore
22

23
        else:
24
            bestScore = float('inf')
25
            # //fill the available colume to an list
26
            availableCol = []
27
            for j in range(7):
28
                if _gameBoard.grids[0][j].value == '':
29
                    availableCol.append(j)
30
            # shuffle the list
31
            random.shuffle(availableCol)
32

33
            for move in availableCol:
34
                possibleBoard = copy.deepcopy(_gameBoard)
35
                possibleBoard.trigger(move)
36
                score = self.minimax(possibleBoard, _depth - 1, True)
37
                bestScore = min(score, bestScore)
38
            return bestScore

Minimax演算法基本上就是將所有可能的落子造成一個tree diagram，而每一層的tree diagram，跟據玩家的交換，一層的分數需要最少化，下一層的分數需要最大化，如此類推，詳細可以看看上面的影片。


xxxxxxxxxx
4
1
 def minimax(self, _gameBoard, _depth, _isMaximizing):
2
        winner = _gameBoard.checkWin()
3
        if winner != None or _depth == 0:
4
            return self.score(winner)

一開始，跟之前一樣，首先檢查有沒有贏、輸或打和，如果這一落子有的話，就可以即時回傳分數。另一個回傳跳出這個minimax()函數的情況是depth==0到底了，這樣回傳的話由於沒有贏家，會回傳None。


xxxxxxxxxx
16
1
if _isMaximizing:
2
            bestScore = float('-inf')
3
            # //fill the available colume to an list
4
            availableCol = []
5
            for j in range(7):
6
                if _gameBoard.grids[0][j].value == '':
7
                    availableCol.append(j)
8
            # shuffle the list
9
            random.shuffle(availableCol)
10

11
            for move in availableCol:
12
                possibleBoard = copy.deepcopy(_gameBoard)
13
                possibleBoard.trigger(move)
14
                score = self.minimax(possibleBoard, _depth - 1, False)
15
                bestScore = max(score, bestScore)
16
            return bestScore

之後這一段就跟上面非常相似了，如果是最大化的case，就將bestScore設定成負無限大，接著便deepcopy一個新的gameboard，將所有可能的步都試行一次，比較特別的是，這次score = self.minimax(possibleBoard, _depth - 1, False)minimax函數我們將函數輸入的_depth減1，函數最後的False是指_isMaximizing，所以如果這次_isMaximizing是True，那下一步就設定成False。


xxxxxxxxxx
16
1
 else:
2
            bestScore = float('inf')
3
            # //fill the available colume to an list
4
            availableCol = []
5
            for j in range(7):
6
                if _gameBoard.grids[0][j].value == '':
7
                    availableCol.append(j)
8
            # shuffle the list
9
            random.shuffle(availableCol)
10

11
            for move in availableCol:
12
                possibleBoard = copy.deepcopy(_gameBoard)
13
                possibleBoard.trigger(move)
14
                score = self.minimax(possibleBoard, _depth - 1, True)
15
                bestScore = min(score, bestScore)
16
            return bestScore

程式的下半部分基本上同，不同的是一開始的bestScore設定成正無限大，而score = self.minimax(possibleBoard, _depth - 1, True)也將最後的_isMaximizing部分設定成True。

這裡minimax()函數入面包裹著minimax()函數，就是我們上面所說的 recursion 遞歸。雖然不是最快的方法，但在編程上會簡潔很多。

5. 令AI懂得阻擋我方


xxxxxxxxxx
23
1
def autoPlay(self):
2
    bestScore = float('inf')
3
    bestMove = random.randint(0, 5)  # the range is a, b+1
4

5
    # //fill the available colume to an list
6
    availableCol = []
7
    for j in range(7):
8
        if self.gameBoard.grids[0][j].value == '':
9
            availableCol.append(j)
10
    # shuffle the list
11
    random.shuffle(availableCol)
12

13
    for move in availableCol:
14
        possibleBoard = copy.deepcopy(self.gameBoard)
15
        possibleBoard.trigger(move)
16
        score = self.minimax(possibleBoard, 1, True)
17
        print(move, score)
18
        if (score < bestScore):
19
            bestScore = score
20
            bestMove = move
21
        print(bestMove)
22
    print('')
23
    self.gameBoard.trigger(bestMove)

當depth = 1:

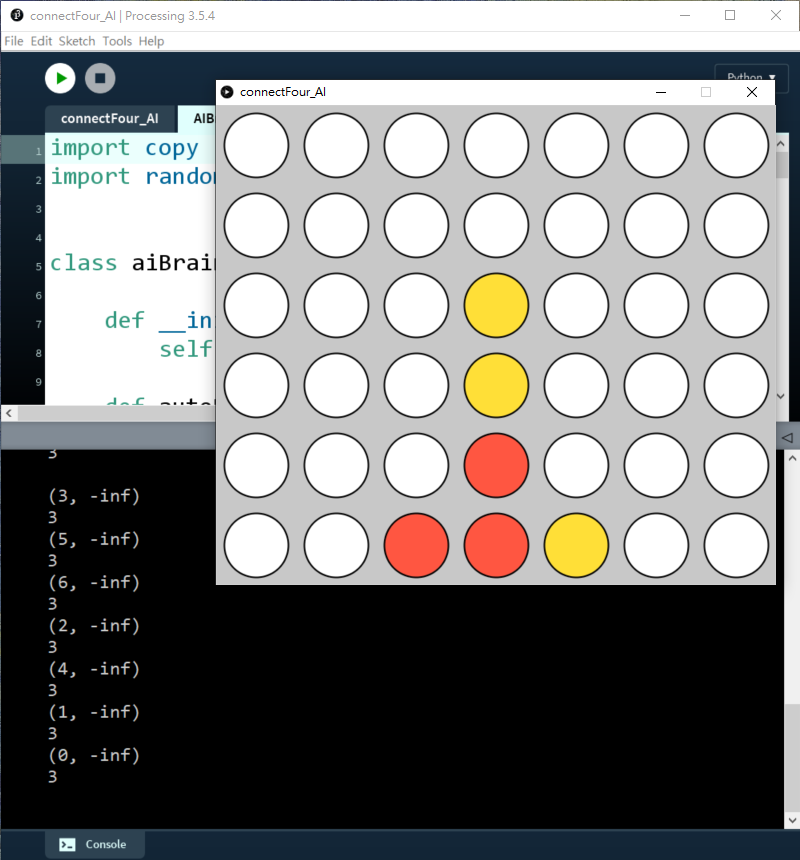
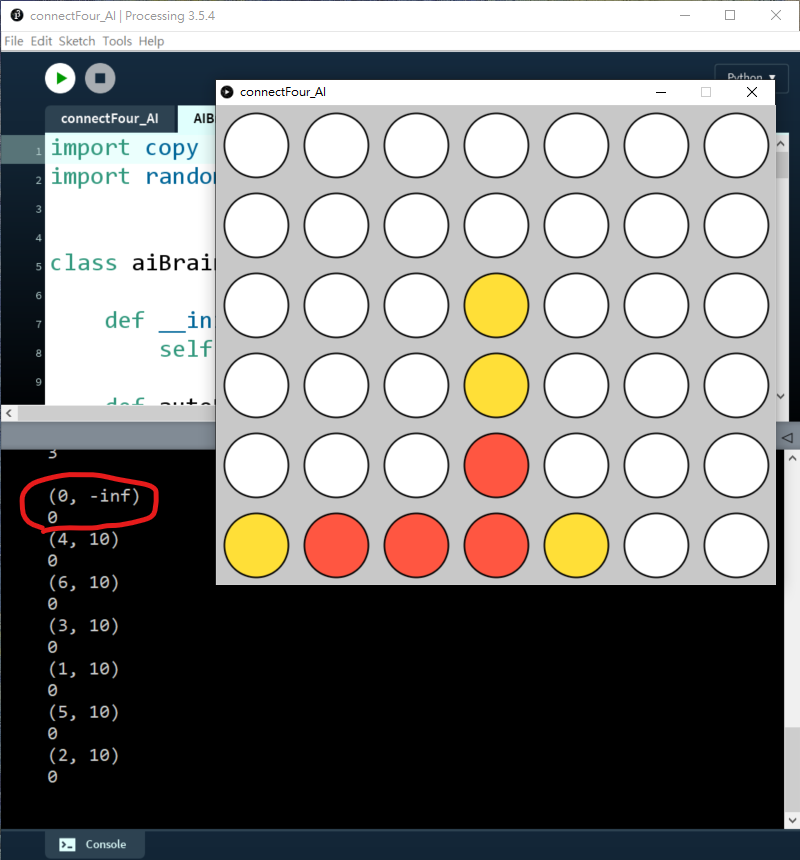
可以見到，如果我落子第2欄(i=1)，AI就會知道我下一步會贏，所以要優先落子第1欄)i=0)

如果進一步將depth = 3:

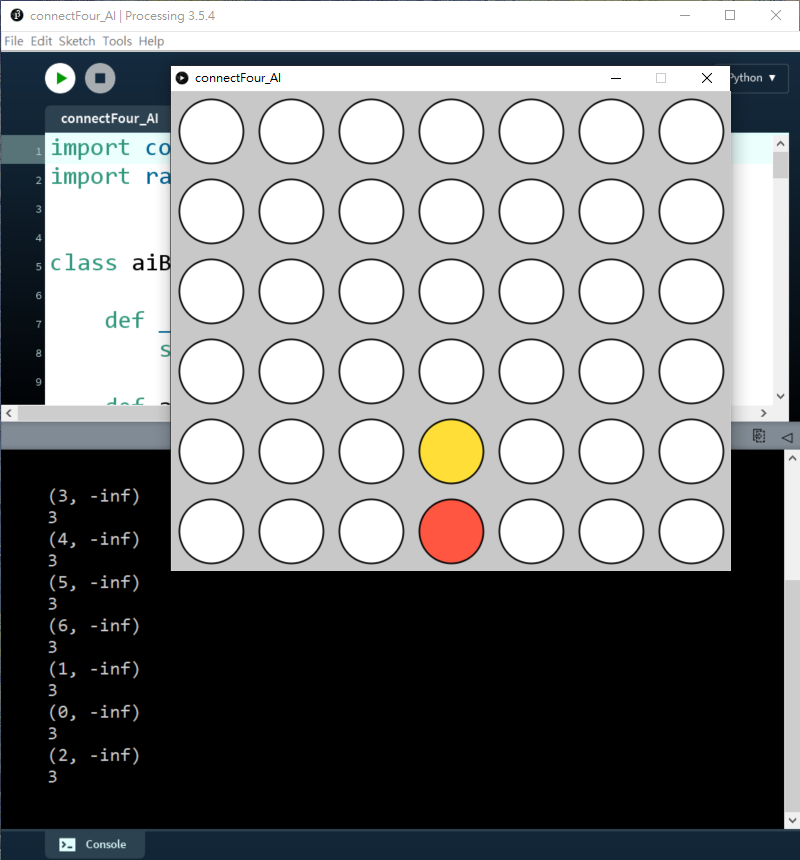
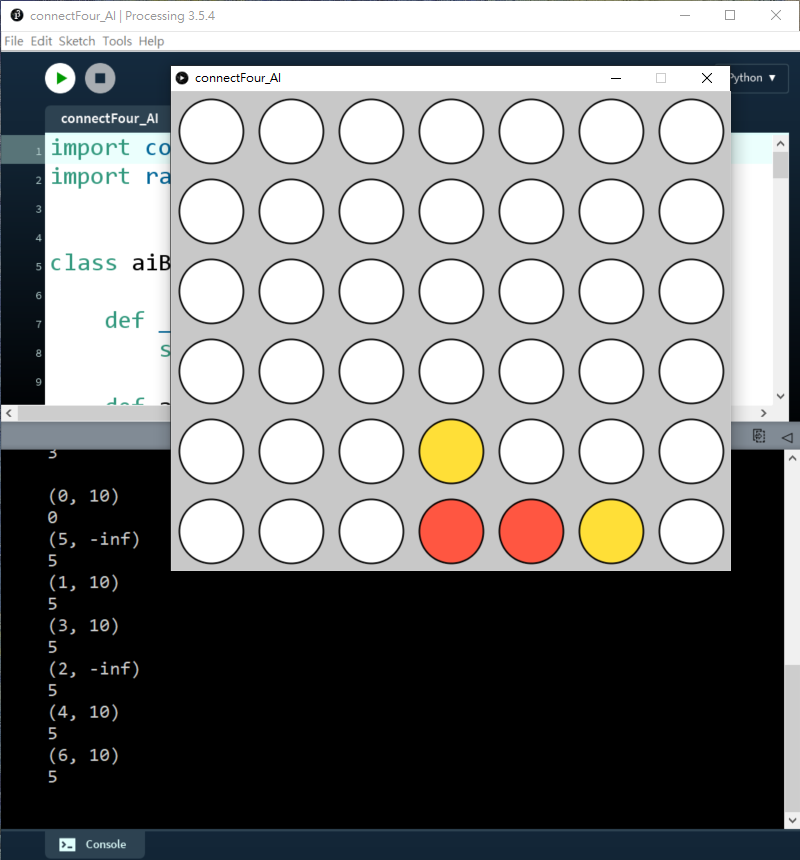
AI甚至懂得防止雙頭蛇，提早在第3欄(i=2)或第6欄(i=6)阻擋我。

上一步的AI之所以不懂阻擋我方，原因是bestScore一開始是設定成負無限大，之後找出最大的bestScore來落子，但我們設定分數時，如果AI方贏的話，分數會是-10分，所以我們找bestScore和bestMove時，找的應該是最小的負數，而不是最大的正數。只要交換，就能正確地令AI懂得防守。

6. 既能阻擋我方，又懂得贏


xxxxxxxxxx
81
1
import copy
2
import random
3

4

5
class aiBrain(object):
6

7
    def __init__(self, _gameBoard):
8
        self.gameBoard = _gameBoard
9

10
    def autoPlay(self):
11
        bestScore = float('inf')
12
        bestMove = random.randint(0, 5)  # the range is a, b+1
13

14
        # //fill the available colume to an list
15
        availableCol = []
16
        for j in range(7):
17
            if self.gameBoard.grids[0][j].value == '':
18
                availableCol.append(j)
19
        # shuffle the list
20
        random.shuffle(availableCol)
21

22
        for move in availableCol:
23
            possibleBoard = copy.deepcopy(self.gameBoard)
24
            possibleBoard.trigger(move)
25
            score = self.minimax(possibleBoard, 1, True)
26
            print(move, score)
27
            if (score < bestScore):
28
                bestScore = score
29
                bestMove = move
30
            print(bestMove)
31
        print('')
32
        self.gameBoard.trigger(bestMove)
33

34
    def score(self, _winner):
35
        if _winner == 'R':
36
            return 10 
37
        elif _winner == 'Y':
38
            return -10 
39
        elif _winner == 'O':
40
            return 0
41
        else:
42
            return 0
43

44
    def minimax(self, _gameBoard, _depth, _isMaximizing):
45
        winner = _gameBoard.checkWin()
46
        if winner != None or _depth == 0:
47
            return self.score(winner)
48

49
        if _isMaximizing:
50
            bestScore = 0
51
            # //fill the available colume to an list
52
            availableCol = []
53
            for j in range(7):
54
                if _gameBoard.grids[0][j].value == '':
55
                    availableCol.append(j)
56
            # shuffle the list
57
            random.shuffle(availableCol)
58

59
            for move in availableCol:
60
                possibleBoard = copy.deepcopy(_gameBoard)
61
                possibleBoard.trigger(move)
62
                score = self.minimax(possibleBoard, _depth - 1, False)
63
                bestScore += score
64
            return bestScore
65

66
        else:
67
            bestScore = 0
68
            # //fill the available colume to an list
69
            availableCol = []
70
            for j in range(7):
71
                if _gameBoard.grids[0][j].value == '':
72
                    availableCol.append(j)
73
            # shuffle the list
74
            random.shuffle(availableCol)
75

76
            for move in availableCol:
77
                possibleBoard = copy.deepcopy(_gameBoard)
78
                possibleBoard.trigger(move)
79
                score = self.minimax(possibleBoard, _depth - 1, True)
80
                bestScore += score
81
            return bestScore

由於經過了minimax()函數後，如果沒有結果，也會回傳-inf，而在比較最少的時間，所有沒有特定結果的case都會全部變了做-inf，所以AI只懂得防守而不懂得進攻。要改良的話方法很簡單，只要將minimax()入面的bestScore設成0，之後在最後比較bestScore的部分，不做min或max，而是改用將所有結果累加。

當depth=1，AI懂得去阻擋我贏

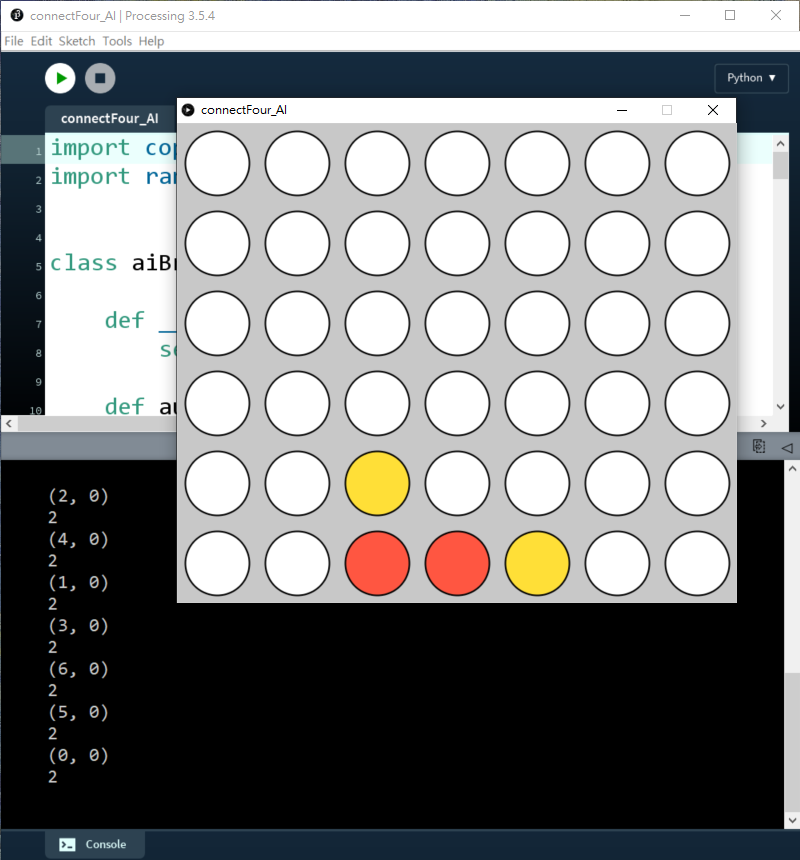
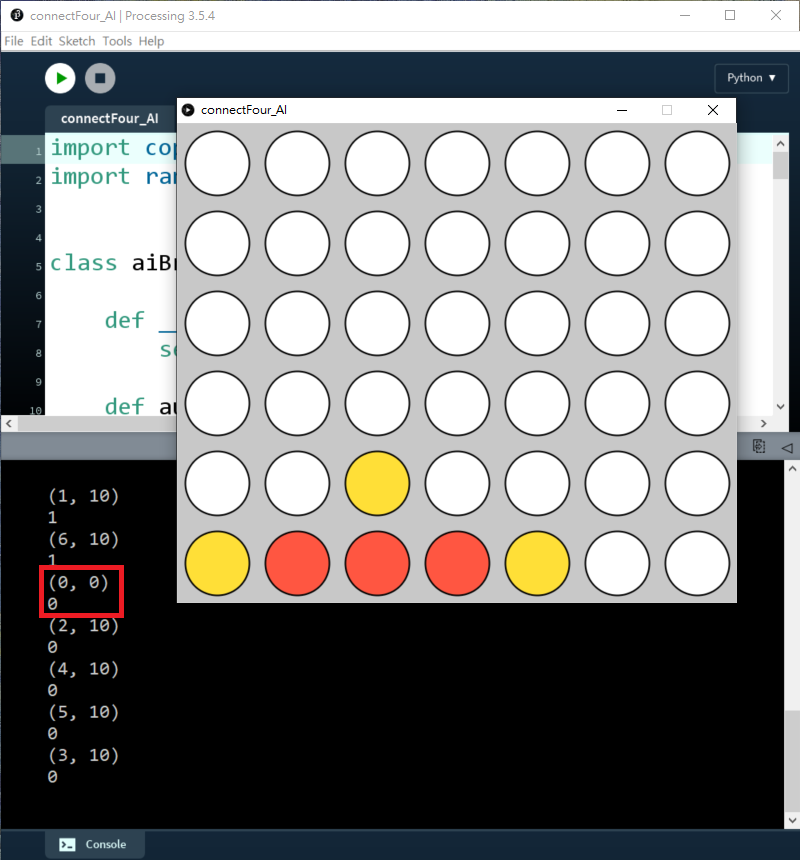
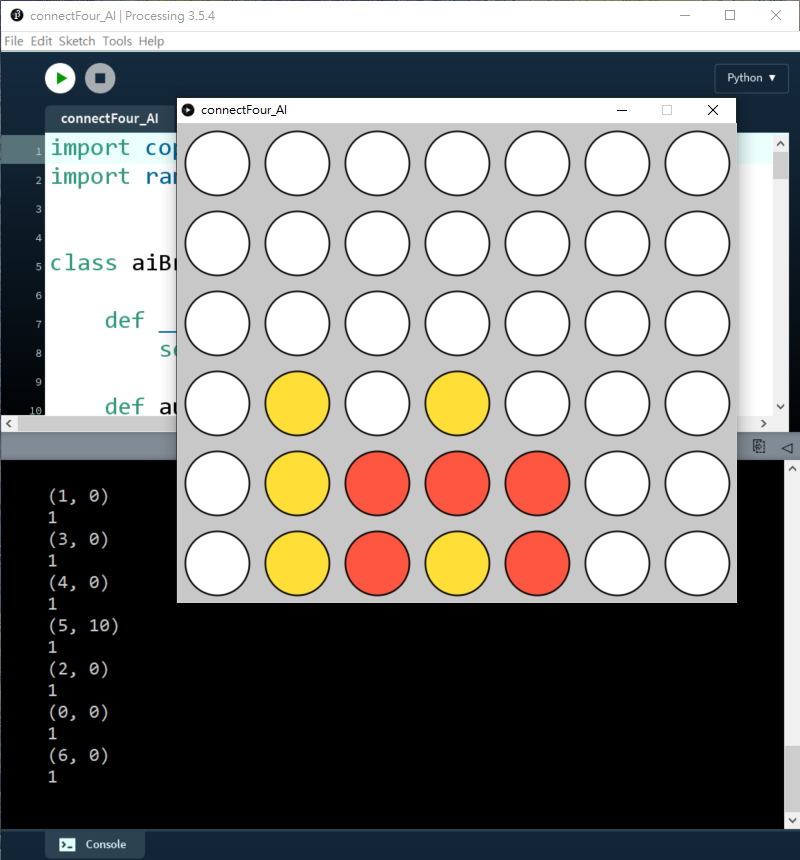
而且也懂得去贏:

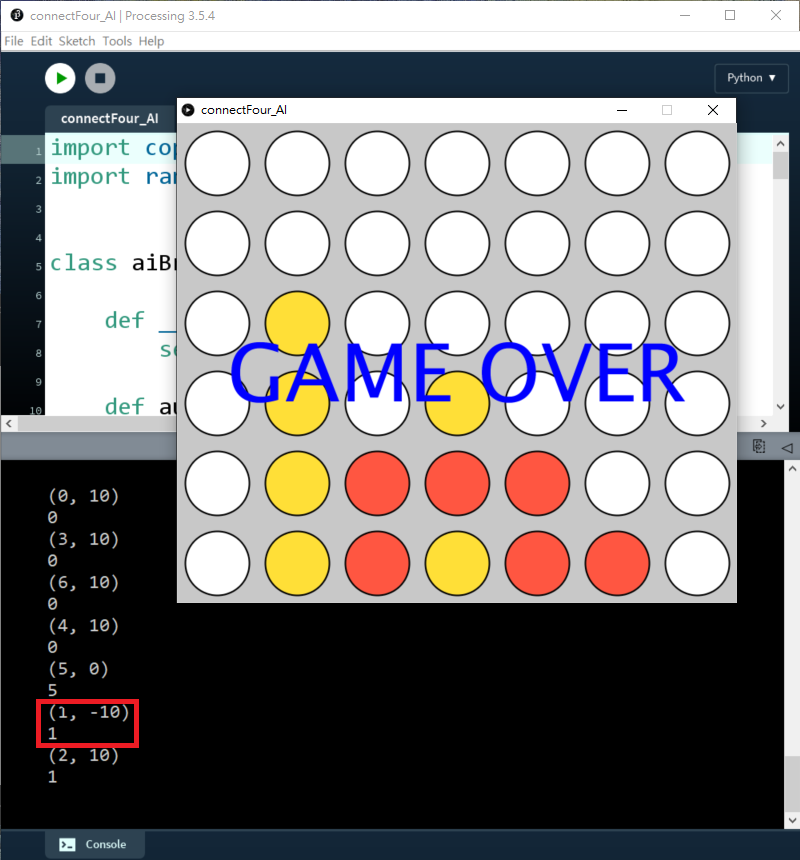
但反而depth=3或以上的話，效果反而一點也不明顯，好似突然變蠢了一樣。如下圖，當depth=3，明明只要下最右手邊的話就會即時贏，AI反而是阻擋我繼續下第三行而不去贏。

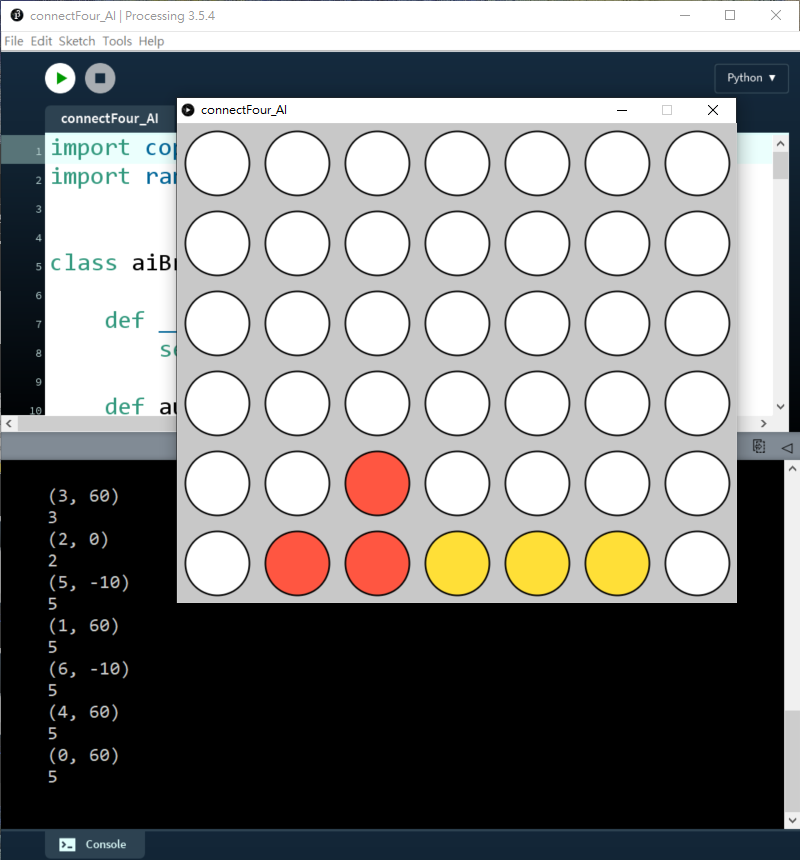
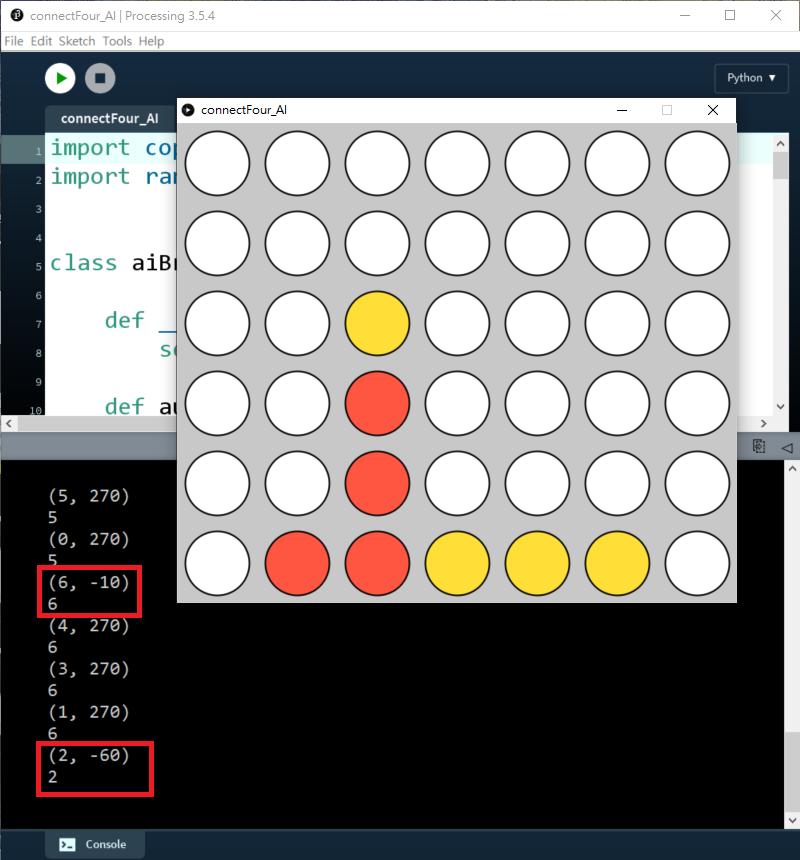
原因是：上述演算法沒有考慮深度的優先，如果下最右手邊(i=6)，遊戲就會即時贏，所以分數只有-10，但如果下第三行(i=2)，由於遊戲未完，演算法會繼續往下兩步(depth=3)，所以會累加之後步的分數，所以反而會比即時贏的分數更少。

普通的minimax演算法，分數是會繼承tree diagram下層的分數，再分min或max，但這樣的方法，如果下一步有即時出現贏或即時輸，它能有效的防守或進攻，但它卻不懂得需要佈局、或走某一步對之後的局面更有利的情況，這是因為minimax演算法缺乏了深度的資訊。例如，minimax對於兩步之後能贏或四步之後才能贏的case，都會給出同等的分數。而我們上面的演算法改了用累加分數，則會累加之後步數，搜尋深度越深分數就會越大。

7. 令分數與`depth`成關係


xxxxxxxxxx
81
1
import copy
2
import random
3

4

5
class aiBrain(object):
6

7
    def __init__(self, _gameBoard):
8
        self.gameBoard = _gameBoard
9

10
    def autoPlay(self):
11
        bestScore = float('inf')
12
        bestMove = random.randint(0, 5)  # the range is a, b+1
13

14
        # //fill the available colume to an list
15
        availableCol = []
16
        for j in range(7):
17
            if self.gameBoard.grids[0][j].value == '':
18
                availableCol.append(j)
19
        # shuffle the list
20
        random.shuffle(availableCol)
21

22
        for move in availableCol:
23
            possibleBoard = copy.deepcopy(self.gameBoard)
24
            possibleBoard.trigger(move)
25
            score = self.minimax(possibleBoard, 3, True)
26
            print(move, score)
27
            if (score < bestScore):
28
                bestScore = score
29
                bestMove = move
30
            print(bestMove)
31
        print('')
32
        self.gameBoard.trigger(bestMove)
33

34
    def score(self, _winner):
35
        if _winner == 'R':
36
            return 10 
37
        elif _winner == 'Y':
38
            return -10 
39
        elif _winner == 'O':
40
            return 0
41
        else:
42
            return 0
43

44
    def minimax(self, _gameBoard, _depth, _isMaximizing):
45
        winner = _gameBoard.checkWin()
46
        if winner != None or _depth == 0:
47
            return self.score(winner) * (10**_depth)
48

49
        if _isMaximizing:
50
            bestScore = 0
51
            # //fill the available colume to an list
52
            availableCol = []
53
            for j in range(7):
54
                if _gameBoard.grids[0][j].value == '':
55
                    availableCol.append(j)
56
            # shuffle the list
57
            random.shuffle(availableCol)
58

59
            for move in availableCol:
60
                possibleBoard = copy.deepcopy(_gameBoard)
61
                possibleBoard.trigger(move)
62
                score = self.minimax(possibleBoard, _depth - 1, False)
63
                bestScore += score
64
            return bestScore
65

66
        else:
67
            bestScore = 0
68
            # //fill the available colume to an list
69
            availableCol = []
70
            for j in range(7):
71
                if _gameBoard.grids[0][j].value == '':
72
                    availableCol.append(j)
73
            # shuffle the list
74
            random.shuffle(availableCol)
75

76
            for move in availableCol:
77
                possibleBoard = copy.deepcopy(_gameBoard)
78
                possibleBoard.trigger(move)
79
                score = self.minimax(possibleBoard, _depth - 1, True)
80
                bestScore += score
81
            return bestScore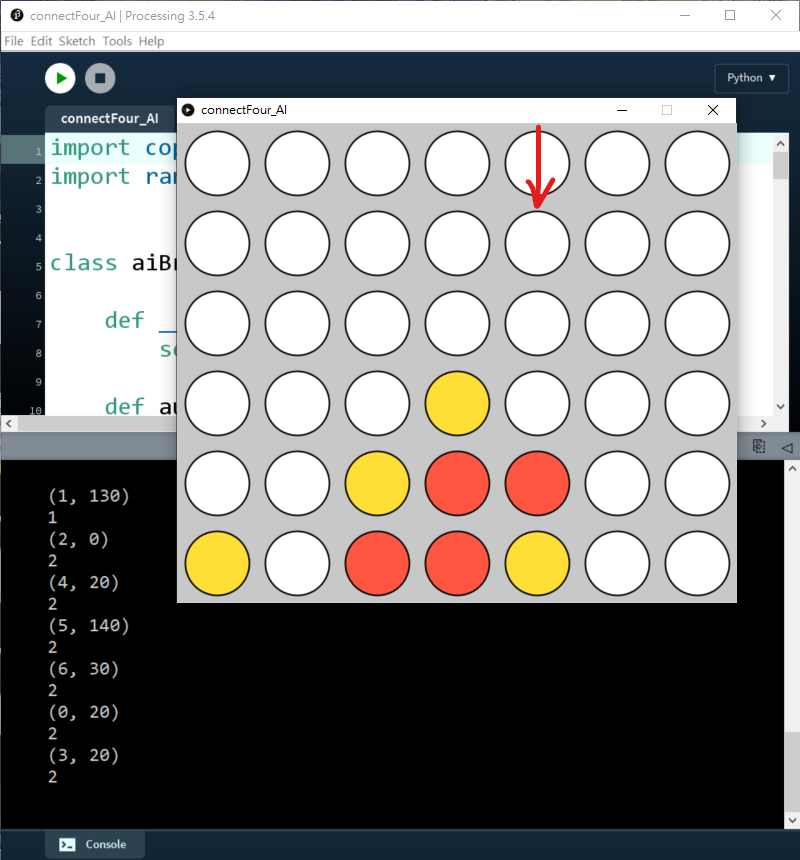


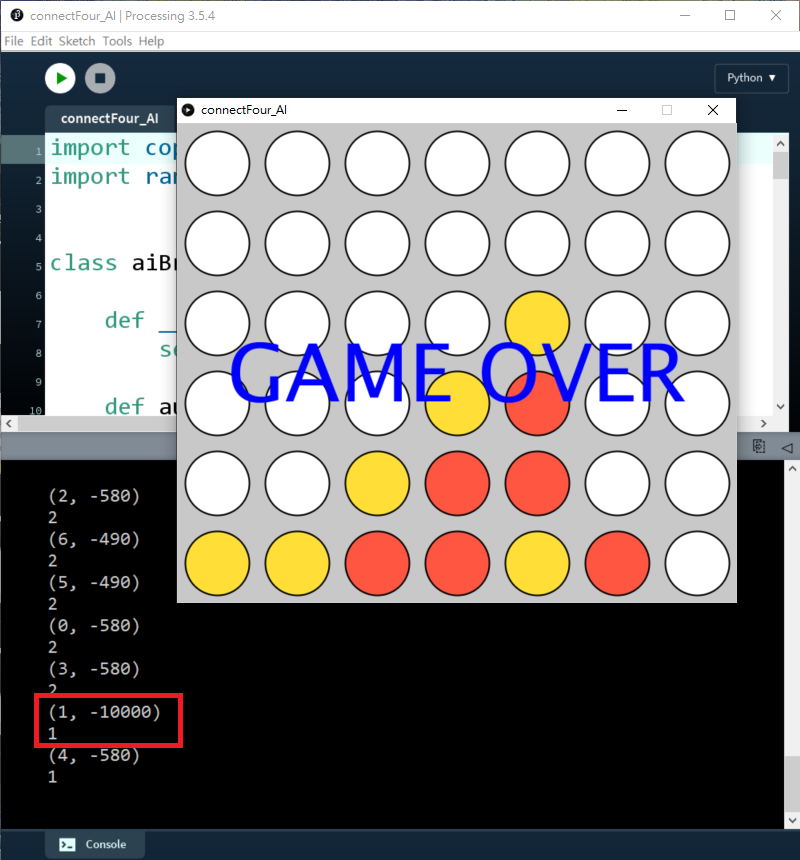
xxxxxxxxxx
4
1
 def minimax(self, _gameBoard, _depth, _isMaximizing):
2
        winner = _gameBoard.checkWin()
3
        if winner != None or _depth == 0:
4
            return self.score(winner) * (10**_depth)

depth=3 $-10\times10^3=10,000$ 分，就會比兩步後再贏多出一個等數級。只要加入這個少少改變，AI就會變得非常厲害，當depth=2時，已經會考慮之後的3步去防守和佈局進攻，如果depth=3時，就會考慮到之後的4步去防守和進攻，已經可以防守和佈置兩頭蛇了。